|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Enseguida se describe la función que cada botón desempeña dentro de la paleta.
B1.
.
Transforma una ecuación lineal de
primer orden
a
la forma de diferenciales (5).
La ecuación puede estar escrita en cualquier de las formas
,
. A manera de ejemplo, transformemos
la ecuación
en una ecuación en diferenciales
totales. Primero, escribimos la ecuación en Mathematica
en la forma
x y’-3 y==x^4.
Después de esto, pinchamos el botón
.
Aparecerá la siguiente ventana de diálogo ( cuaderno emergente) :
En
nuestro caso,
x
es la variable independiente
y
y
es la variable dependiente. Después
de llenar las respectivas casillas y pinchar el botón
Mathematica 4.1 nos proporciona
lo siguiente :
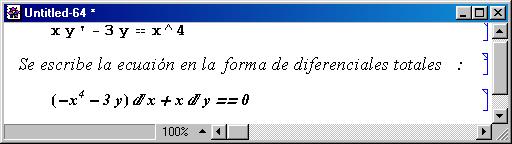
Inmediatamente
aparece el resultado, Mathematica lo sombrea ( es decir, el botón se programa
de manera que la selección se mueva al resultado que proporciona el botón que
se acaba de ejecutar).
B2.
.
Este botón se aplica a ecuaciones de la forma
(5), es decir, a ecuaciones en diferenciales totales. Si la ecuación es
exacta, la integra como tal. El programa implementado en este botón verifica la
condición (7) , la cual en caso de cumplirse, aplica las fórmulas (8), (9) y
(10) para integrar la ecuación. A manera de ejemplo, consideremos la ecuación
exacta
. Inicialmente se introduce esta ecuación en Mathematica en la forma
(y^2+6
x y+2 x^2)*Dt[x]+(4 y^2+2 x y+3 x^2)*Dt[y]==0
Al
pinchar el botón
aparece
la ventana de diálogo que nos pregunta acerca de las variables independiente y
dependiente, las cuales en nuestro caso son
e
, respectivamente. Llenamos las casillas correspondientes, como se aprecia a
continuación :
