|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1.1.3. Factores integrantes.
Cuando
la ecuación (5) no es exacta, algunas veces es posible obtener una función
tal que si se multiplican ambos
lados de la ecuación (5) por esta función, entonces se obtiene una ecuación
exacta. Tal función se llama factor integrante de la ecuación. La condición de exactitud
equivale a encontrar al menos una
función
que satisfaga la siguiente ecuación
diferencial en derivadas parciales :
.
Sin embargo, esta ecuación puede resultar tanto o más difícil de resolver que la ecuación (5). Existen casos especiales que permiten encontrar un factor integrante, los cuales se describen a continuación :
I.
La expresión
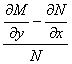depende solamente de
, digamos, es igual a 
. Un factor integrante es
. Este es el caso de la ecuación lineal
, para la cual
y
. Al multiplicar ambos lados de esta ecuación por
se obtiene una ecuación exacta.
II.
La expresión
depende solamente de
y
, digamos, es igual a
h(y)
. Un factor integrante es
.
III.
La expresión
es una función del producto
o de la suma
. Un factor integrante es
.
IV.
Las funciones
M(x,y)
y
N(x,y)
son homogéneas y del mismo
grado, es decir, existe
n
tal que
y
. Un factor integrante es
, siempre y cuando
.
Cabe anotar que al hacer la sustitución y = ux , siendo u = u(x) , se obtiene una ecuación en variables separables.
V. Las funciones M y N satisfacen las ecuaciones de Cauchy –Riemann en cierta región del plano xy , de modo que
y
.
Un factor
integrante es
.
VI.
Las funciones
M
y
N
se pueden representar en la forma
y
, en donde
. En este caso, un factor integrante es
, siempre y cuando
.
VII.
La expresión
puede representarse en la forma
. Un factor integrante se puede buscar en la forma
. En este caso, se puede tomar
y
.