|
|
Históricamente, el estudio de las soluciones de las ecuaciones diferenciales ordinarias (EDO por comodidad) se ha desarrollado en tres grandes escenarios: el algebraico, el numérico y el geométrico. Desde la perspectiva de la enseñanza, los programas de estudio y los libros de texto nos muestran, por diversas razones, un predominio del escenario algebraico (con sus variantes), con algunos atisbos de los acercamientos numérico y geométrico. Esto ha traído como consecuencia, que se tenga una visión muy parcial de los métodos que existen para resolver EDO, pues frecuentemente en el estudio de los modelos determinísticos (v.gr. electrónica, óptica, etc.) se requiere establecer “articulaciones” entre los diferentes acercamientos. Usando la Historia de la Matemática como base para la Transposición Didáctica se presenta, en este trabajo, una experiencia en la impartición de las EDO, en la Licenciatura en Educación, especialidad Física-Electrónica de la Universidad Pedagógica de Holguín, en la cual se integran los tres escenarios de solución de las mismas y se modifica el esquema de enseñanza actual de dicha asignatura. Esta experiencia sirvió de base para la tesis del Programa de Maestría "Didáctica de la Matemática", defendida por el segundo autor, bajo la dirección del primero. Una vía para modificar este esquema de enseñanza, es el juego de marcos introducidos por Douady (1986). Un marco, como ella nos dice, se entiende en el sentido usual que tiene cuando hablamos del marco algebraico, del marco aritmético, del marco geométrico; en el “juego de marcos” el docente propone al estudiante cambios entre los distintos tipos de marcos respecto a los problemas escogidos a conveniencia, con el fin de que ellos avancen en las fases del problema y que sus conocimientos evolucionen. En el trabajo, estudiamos cómo se pueden incorporar estas ideas, en particular en la enseñanza de las EDO[1], donde los escenarios son ejemplos de los marcos, asimismo, propondremos problemas con el fin de ver cómo se puede generar el juego de marcos; donde en este “juego” la computadora personal (PC) va a desempeñar un papel central. Douady introduce la noción de marco en su tesis doctoral en el siguiente sentido: “Digamos
que un marco está constituido por objetos de una rama de las matemáticas, por
las relaciones entre los objetos, por sus formulaciones eventualmente diversas
y por imágenes mentales asociadas a esos objetos y sus relaciones. Estas
imágenes juegan un papel esencial en su funcionamiento como útiles, de los
objetos del marco. Dos marcos pueden tener los mismos objetos mas diferir en
las imágenes mentales y la problemática desarrollada... concebimos la noción de marco, como una
noción dinámica. El cambio de marcos es un medio para obtener formulaciones
diferentes de un problema que sin ser necesariamente equivalentes permiten un
nuevo acercamiento a las dificultades encontradas y la puesta en escena de
útiles y técnicas que no se impusieron en la primera formulación”. Más adelante introduce el “juego de marcos”, como el cambio de marcos propuesto por el docente para hacer avanzar las fases de investigación de un problema en una situación escolar. En el desarrollo de este juego se distinguen tres fases: 1.
Transferencia e interpretación. 2.
Correspondencias imperfectas. 3.
Mejoramiento de la correspondencia y progreso del conocimiento. En nuestro caso, los distintos escenarios de solución de las EDO, son ejemplos de los marcos, así hablaremos de los marcos algebraico, numérico y geométrico en el mismo sentido que los escenarios algebraico, numérico y geométrico. El juego de marcos es proponer a los alumnos resolver una cierta EDO en un cierto marco y traducirlo (todo o parte de éste) a otro (transferencia e interpretación). La correspondencia entre los marcos en general es imperfecta, ya sea por causa matemática o por conocimientos insuficientes de los estudiantes. Esta situación es fuente de desequilibrio, a su vez la comunicación entre los marcos y, en particular, la comunicación con un marco auxiliar de representación es un factor de reequilibración. Esto conduce al mejoramiento de las correspondencias y al progreso del conocimiento (ver Douady (1986)). Para fijar ideas, consideremos el problema de resolver una simple EDO:
Este mismo problema se puede plantear como la solución de un sistema (donde se introduce una tercera variable, el tiempo t) o bien de una EDO de segundo orden con coeficientes constantes, es decir, poniendo x = x(t), y = y(t) obtenemos:
es decir, el sistema:
Al derivar la
segunda ecuación del sistema obtenemos
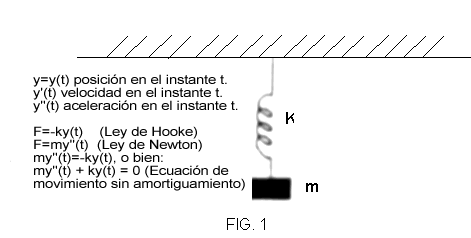
La ecuación (3) es interesante, ya que representa la ecuación de un sistema masa-resorte (donde la masa y la constante del resorte son iguales a 1) sin amortiguamiento, que conduce a “oscilaciones libres” (ver fig. 1). En virtud de la equivalencia de las tres
ecuaciones, establecer la ecuación del movimiento para este caso, es
equivalente a resolver la ecuación (1), la cual es de variables separables y conduce a una solución de la forma x2
+ y2=c, esta ecuación representa una familia de circunferencias
con centro en el origen y radio
En este caso, la solución del problema seguiría en general el siguiente esquema: Modelo ® EDO ® Marco
(algebraico, numérico, geométrico) ® Representación (gráfica, numérica, geométrica) ® Solución ® Modelo. En este camino, algunas etapas de las rutas tienen
dos o más subrutas, como se muestra en el Anexo 2. Revista
Virtual, Matemática Educación e Internet. |
, lo que nos lleva a conjeturar que 
. De lo anterior podemos observar que “inducir la solución”
requiere, en principio, de la articulación de