|
|
La articulación de los marcos numérico,
algebraico y gráfico en la Matemática. El caso
de las ecuaciones diferenciales ordinarias Este tema como
ningún otro quizás se preste para la unión de los enfoques antes citados. Si partimos de definir cada uno de sus
entornos, tendremos que
los programas actuales
constan, casi exclusivamente, del
enfoque
algorítmico-algebraico. Los componentes geométricos (de la teoría
cualitativa) y numéricos están
prácticamente desaparecidos, si contamos con un equipamiento aceptable, es lógico que se impone la pregunta ¿cómo remediar esta
situación?. Desde el
punto de vista histórico, el primer entorno donde se
desarrolló la teoría de las
ecuaciones diferenciales ordinarias
es el algebraico, multitud de intentos brindaron los métodos conocidos hoy,
muchos de los cuales tienen
unos cuantos años (Hernández
(1994)). Si a esto sumamos que en el
año 1992 se cumplieron 100 años de la
Teoría Cualitativa, vinculada
su nacimiento con las
obras "Los Nuevos
Métodos de la Mecánica Analítica" (Poincaré) y "Problema General de la Teoría
de la Estabilidad del
Movimiento" (Liapunov), tendremos bien a las claras que un estudio cualitativo es
siempre útil, máxime cuando el modelo
analizado puede ser no
lineal, en cuyo
caso es imprescindible prácticamente. Por otra parte, el desarrollo de los modernos ordenadores, ha hecho posible la implementación
de métodos numéricos con
una rapidez de convergencia sumamente elevada, de ahí la posibilidad de la utilización de
los mismos. Todo trabajo de teorización o de ingeniería didáctica de las matemáticas presupone y utiliza, necesariamente, un modelo más o menos elaborado (aunque a menudo implícito) de la actividad matemática y asimismo, una noción de lo que es «enseñar y aprender matemáticas». La explicitación de estos modelos permite que sean cuestionados, contrastados empíricamente y reelaborados, por lo que debería constituir un punto de referencia en toda investigación de didáctica de la Matemáticas (Bosch y Gascon (1994)). En nuestra experiencia, seguimos la metodología dada por Douady en su trabajo “La ingeniería didáctica, un instrumento privilegiado para tomar en cuenta en la complejidad de la clase”, la cual se compone de tres ejes estudios: a) Análisis a priori. b) Concepción de una enseñanza, es decir, la ingeniería didáctica propiamente dicha. c) Análisis de los productos de la experiencia. En el caso de nuestra experiencia, la parte a) corresponde fundamentalmente al análisis de los distintos aspectos que hemos creído necesario tomar en cuenta: la historia de las edo, la evolución de los libros de textos, el impacto de las nuevas tecnologías, las creencias y concepciones de los profesores sobre la Matemática, etc. Una primera actitud es precisamente la de mencionar que las EDO nos sirven, fundamentalmente, para modelar problemas cuya esencia es objeto de estudio por una rama de la ingeniería o de las ciencias: física, química, economía, etc. La primera dificultad que se nos presenta, es que no se puede considerar el fenómeno en estudio exactamente como se presenta en la Naturaleza, debido a la gran cantidad de aspectos que habría que tener en cuenta y a la consecuente necesidad de conocimientos matemáticos demasiados complejos, lo cual trae como consecuencia la idealización del problema en el cual no se consideran aquellos aspectos del fenómeno que no tienen gran influencia en el objeto de estudio, aquí es importante la presencia de especialistas de la rama. Por ejemplo, si se quiere describir el movimiento de un péndulo, es posible que el peso de la cuerda sea insignificante en el proceso. Para la modelación y solución es importante tener en cuenta el siguiente proceder: 1. Determinar las funciones que relacionan las magnitudes esenciales que caracterizan el proceso. 2.
Utilizar las leyes de la ciencia a la cual corresponde el problema en
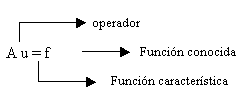
estudio, para describir el proceso mediante ecuaciones. Por lo general se
puede representar en la forma:
3. Determinar las condiciones adicionales
que caracterizan completamente el
proceso. Entre estas condiciones, son frecuentes las llamadas condiciones
iniciales que caracterizan el inicio del proceso y las llamadas condiciones
de contorno, que caracterizan el comportamiento del fenómeno objeto de
estudio, durante el proceso en la frontera de la región en la cual ocurre. Antes de pasar a la búsqueda de su solución,
debemos comprobar algunos aspectos que impone el problema real: 4. Estudio de la existencia y unicidad de la solución. Por ejemplo, si estudiamos, el lanzamiento de un proyectil por un arma de artillería a partir de su velocidad inicial y del conocimiento de la resistencia del aire y pretendemos determinar la trayectoria del proyectil y la posición de este en cualquier tiempo, obligatoriamente el sistema de ecuaciones diferenciales que forma parte del modelo matemático correspondiente debe tener solución; porque realmente al lanzar el proyectil y transcurrir cierto tiempo después de lanzado, este debe ocupar una posición en el espacio. Si contrariamente a lo que nos indica la práctica, el modelo matemático no tiene solución, es porque se ha cometido un error en su formulación. Los procesos físicos, químicos, etc., que se modelan por ecuaciones diferenciales siempre tienen solución única. 5. Continuidad de la solución con respecto a las condiciones adicionales. Las condiciones adicionales que caracterizan completamente un proceso de la Naturaleza, se determinan, en general, por vía experimental y por ello no siempre son exactas. Es importante señalar que el estudio de la existencia, la unicidad y la dependencia continua de la solución de las condiciones adicionales, no solo es parte importante de la modelación del problema; en algunos problemas reales, puede ser de hecho parte esencial o total de la solución. 6. Determinación de la solución. En la teoría de ecuaciones diferenciales pueden distinguirse tres tipos de métodos; los llamados métodos analíticos, con los cuales se determina la solución de las ecuaciones diferenciales de forma exacta, o al menos en cuadraturas; los métodos numéricos, con los cuales la solución se determina aproximadamente; y los métodos cualitativos, con los cuales se investigan las propiedades deseadas de la solución, en muchos casos, sin necesidad de obtenerlas. En este punto es donde radica el peso fundamental de nuestra propuesta. 7. Determinación de una cota para el error. La solución aproximada se busca, generalmente, mediante un proceso iterativo y en ese caso es importante obtener, al menos, una valoración del error en función del número de iteraciones. 8. Análisis de la
estabilidad de la solución. Revista
Virtual, Matemática Educación e Internet. |