|
Las reglas de divisibilidad por un entero 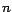 que aquí discutimos
parten todas de la representación decimal del número que aquí discutimos
parten todas de la representación decimal del número 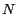 cuya
divisibilidad por cuya
divisibilidad por 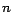 deseamos investigar. En otras palabras, todas estas
reglas se basan en manipulaciones de los dígitos del dividendo deseamos investigar. En otras palabras, todas estas
reglas se basan en manipulaciones de los dígitos del dividendo 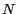 ,
expresado decimalmente. La regla más sencilla y trasparente es,
lógicamente, la de divisibilidad por 10. Un número es divisible por
10 si y solo si su último digito es 0. La demostración es trivial,
pero la formularemos rigurosamente porque ilustra el tipo de razonamiento
que utilizaremos más adelante para obtener reglas de divisibilidad más
complejas. ,
expresado decimalmente. La regla más sencilla y trasparente es,
lógicamente, la de divisibilidad por 10. Un número es divisible por
10 si y solo si su último digito es 0. La demostración es trivial,
pero la formularemos rigurosamente porque ilustra el tipo de razonamiento
que utilizaremos más adelante para obtener reglas de divisibilidad más
complejas.
En nuestra discusión utilizaremos repetidamente los siguientes
resultados sencillos: Si 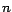 y y 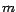 son dos enteros, ambos divisibles por
otro entero son dos enteros, ambos divisibles por
otro entero 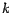 , entonces , entonces 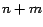 es divisible por es divisible por 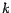 . Y si . Y si 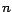 es
divisible por es
divisible por 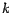 , pero , pero 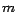 no lo es, entonces no lo es, entonces 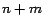 no es divisible por no es divisible por
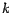 . Ambos resultados son muy fáciles de demostrar (lo cual dejamos
como ejercicio para el lector interesado) y pueden resumirse así:
Supongamos que . Ambos resultados son muy fáciles de demostrar (lo cual dejamos
como ejercicio para el lector interesado) y pueden resumirse así:
Supongamos que 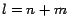 y que y que 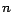 es un entero divisible por es un entero divisible por 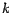 . En ese
caso . En ese
caso  es divisible por es divisible por 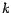 si y solo si si y solo si 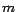 también es divisible por también es divisible por
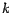 . .
De ahora en adelante utilizaremos la notación 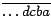 para denotar el
número con la expresión decimal dada por el dígito para denotar el
número con la expresión decimal dada por el dígito 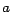 en el
lugar de las unidades, el dígito en el
lugar de las unidades, el dígito 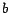 en el lugar de las decenas, etc.
Por lo tanto, el valor de en el lugar de las decenas, etc.
Por lo tanto, el valor de 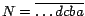 puede expresarse de la siguiente
manera: N = a + 10b + 100c + 1000d + ... puede expresarse de la siguiente
manera: N = a + 10b + 100c + 1000d + ...
Demos a la cantidad
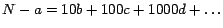 el nombre el nombre 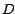 .
Evidentemente, .
Evidentemente, 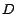 siempre será divisible por 10, sin importar los
valores de siempre será divisible por 10, sin importar los
valores de
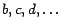 Como Como 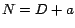 , concluimos que , concluimos que 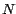 es
divisible por 10 si y solo si es
divisible por 10 si y solo si 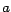 es divisible por 10. El número es divisible por 10. El número 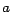 debe estar entre 0 y 9 inclusive, y de esos valores únicamente 0 es
divisible por 10, (recordemos que 0 es divisible por cualquier número
entero
debe estar entre 0 y 9 inclusive, y de esos valores únicamente 0 es
divisible por 10, (recordemos que 0 es divisible por cualquier número
entero 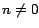 , puesto que , puesto que 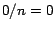 ). Por lo tanto, ). Por lo tanto, 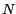 es
divisible por 10 si y solo si es
divisible por 10 si y solo si 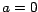 . .
Esta demostración puede ser modificada inmediatamente para formular y
demostrar la regla de divisibilidad para cualquier divisor del número
10, puesto que si 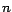 divide a 10, necesariamente divide a divide a 10, necesariamente divide a 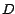 . Por lo
tanto . Por lo
tanto 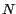 es divisible por 2 (o por 5) si y solo si el último
dígito es divisible por 2 (o por 5) si y solo si el último
dígito 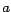 es divisible por 2 (o por 5). Para el 2, esto implica que es divisible por 2 (o por 5). Para el 2, esto implica que
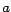 debe ser par. Para el 5, implica que debe ser par. Para el 5, implica que 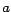 debe ser 0 o 5. debe ser 0 o 5.
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|