|
El lector acucioso se habrá percatado, por nuestra discusión anterior,
que la lógica de las reglas de división es la siguiente: La regla nos
indica que formemos cierto número 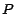 a partir de una manipulación con
los dígitos de a partir de una manipulación con
los dígitos de 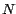 en su expresión decimal en su expresión decimal 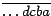 . Si podemos
demostrar que . Si podemos
demostrar que 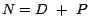 y que y que 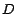 siempre es divisible por siempre es divisible por 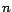 ,
tendremos que ,
tendremos que 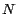 es divisible por es divisible por 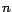 si y solo si si y solo si 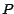 es divisible por es divisible por
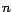 . Y como, para un número . Y como, para un número 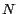 arbitrario, tenemos que arbitrario, tenemos que 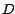 puede
corresponder a una suma con cualquier cantidad de términos, la
demostración de que puede
corresponder a una suma con cualquier cantidad de términos, la
demostración de que 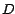 es divisible por es divisible por 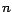 suele depender de que cada
uno de los términos en esa suma sea, por sí solo, divisible por suele depender de que cada
uno de los términos en esa suma sea, por sí solo, divisible por
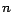 5. 5.
Si 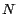 es tan grande que es tan grande que 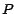 es un número cuya divisibilidad no nos
resulta obvia, podemos aplicar la regla nuevamente para es un número cuya divisibilidad no nos
resulta obvia, podemos aplicar la regla nuevamente para 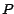 , y repetir
este proceso tantas veces como necesitemos para acabar con un número tan
pequeño que su divisibilidad sea obvia. Por ejemplo, supongamos que
queremos saber si , y repetir
este proceso tantas veces como necesitemos para acabar con un número tan
pequeño que su divisibilidad sea obvia. Por ejemplo, supongamos que
queremos saber si 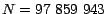 es divisible por 9. Al aplicar la regla
de divisibilidad tenemos que es divisible por 9. Al aplicar la regla
de divisibilidad tenemos que 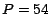 . Si se no hubiera olvidado que . Si se no hubiera olvidado que
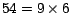 , podemos aplicar la regla una segunda vez, lo cual nos da , podemos aplicar la regla una segunda vez, lo cual nos da
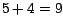 . En dos pasos hemos pasado de un número de 8 dígitos a
uno un solo dígito. La regla de divisibilidad por 9 es sumamente
eficiente, pues cada aplicación reduce un número . En dos pasos hemos pasado de un número de 8 dígitos a
uno un solo dígito. La regla de divisibilidad por 9 es sumamente
eficiente, pues cada aplicación reduce un número 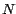 a un número a un número 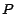 mucho menor.
mucho menor.
La regla de divisibilidad por 10 es aún más eficiente: reduce, en un
solo paso, un número 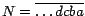 de cualquier cantidad de dígitos, a
un número de cualquier cantidad de dígitos, a
un número 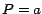 de un solo dígito. Hoy, en la era en que las
computadoras y las calculadores de bolsillo abundan en gran parte del
mundo, dividir un entero por otro podría no parecer una tarea muy
difícil. Pero esto no debiera cegarnos a la belleza conceptual de la
eficiencia con la que las reglas que hemos presentado simplifican el
problema de saber si un número es divisible por otro. de un solo dígito. Hoy, en la era en que las
computadoras y las calculadores de bolsillo abundan en gran parte del
mundo, dividir un entero por otro podría no parecer una tarea muy
difícil. Pero esto no debiera cegarnos a la belleza conceptual de la
eficiencia con la que las reglas que hemos presentado simplifican el
problema de saber si un número es divisible por otro.
Si lo deseamos, podemos cuantificar la eficiencia de las reglas de
divisibilidad de la siguiente manera. Si 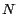 es un número de es un número de  dígitos, en el peor de los casos, ¿cuántos dígitos esperamos
que tenga el número
dígitos, en el peor de los casos, ¿cuántos dígitos esperamos
que tenga el número 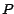 ? La regla del diez es tan eficiente como puede
ser: ? La regla del diez es tan eficiente como puede
ser: 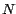 puede tener cualquier número de dígitos y puede tener cualquier número de dígitos y 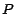 siempre
tendrá un solo dígito. El caso de la regla para el 9 es
ligeramente más sutil. El tamaño de siempre
tendrá un solo dígito. El caso de la regla para el 9 es
ligeramente más sutil. El tamaño de 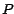 depende de los dígitos
específicos de depende de los dígitos
específicos de 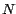 . Pero un dígito decimal no puede ser mayor
que 9. Esto es, . Pero un dígito decimal no puede ser mayor
que 9. Esto es, 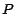 para un número para un número 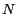 de de 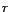 dígitos es siempre
igual o menor que dígitos es siempre
igual o menor que 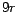 . Aquellos lectores que conozcan la teoría de
los logaritmos sabrán que el número de dígitos en la
representación decimal de . Aquellos lectores que conozcan la teoría de
los logaritmos sabrán que el número de dígitos en la
representación decimal de 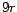 está dado por uno más la parte entera
de está dado por uno más la parte entera
de 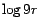 y que la parte entera de y que la parte entera de 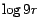 es igual o menor que 1
más la parte entera de es igual o menor que 1
más la parte entera de 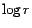 . .
Por lo tanto, en el caso de la regla de divisibilidad por 9, el número
de dígitos de 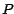 es igual o menor que 2 más el logaritmo del número
de dígitos de es igual o menor que 2 más el logaritmo del número
de dígitos de 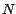 . Un estudioso de la teoría de la computación
diría que la regla de divisibilidad por 9 tiene una "eficiencia logarítimica.'' . Un estudioso de la teoría de la computación
diría que la regla de divisibilidad por 9 tiene una "eficiencia logarítimica.''
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|