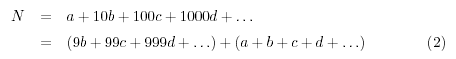Reglas de divisibilidad		Alejandro Jenkins V.

Inicio  1  2  3  4  5  6  7  8  9  10  11  12

 

Divisibilidad por 9 y 3

La regla de divisibilidad por 9 es mucho más sorprendente y seguramente ha intrigado a un sinnúmero de estudiantes de escuela primaria, como intrigó al joven Georges Perec (quien más tarde se convertiría en uno de los escritores franceses más originales del siglo XX).

Un número es divisible por 9 si y solo si la suma de sus dígitos es divisible por 9. La demostración es la siguiente:

Supongamos que $N = \cba$. Entonces

Llamaremos $D$ a la cantidad $9b + 99c + 999d + \ldots$ en la ecuación (2), de manera que $N = D + a + b + c + d + \ldots$ Está claro que $D$ siempre es divisible por 9 ². Por lo tanto $N$ es divisible por 9 si y solo si $a + b + c + d + \ldots$ (o sea, la suma de sus dígitos) es divisible por 9.

Fácilmente podemos modificar este resultado para formular y demostrar una regla de divisibilidad por el único divisor propio de 9: el número 3. $D=9b + 99c + 999d + \ldots$ es siempre divisible por 3. Por lo tanto un número es divisible por 3 si y solo si la suma de sus dígitos es divisible por 3.

A partir de las reglas que hemos cubierto hasta aquí, podemos inmediatamente formular varias otras. Un número es divisible por 6 si y solo si es divisible por 2 y por 3. Un número es divisible por 4 si y solo si sus últimos dos dígitos forman un número (el número $\overline{ba}$) divisible por 4. Dejamos al lector como ejercicio sencillo formular y demostrar una regla de divisibilidad para el 8.

 

Inicio  1  2  3  4  5  6  7  8  9  10  11  12

Cidse - Revista virtual Matemática, Educación e Internet - ITCR
Derechos Reservados