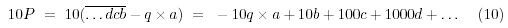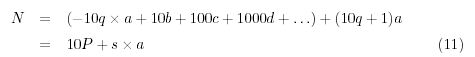Reglas de divisibilidad

  

Alejandro Jenkins V.
   
 Inicio  1  2  3  4  5  6  7  8  9  10  11  12

 

 

Divisibilidad por $n>10$

Resulta evidente que las reglas de división para el 13 que hemos formulado representan el fruto de la desesperación, puesto que en la gran mayoría de los casos el cálculo para obtener $P$ es complicado y debe repetirse varias veces antes de alcanzar un número cuya divisibilidad sea evidente. Usando el lenguaje de la sección anterior, podemos decir que las reglas son no solo complicadas, sino además ineficientes.

Pero estas reglas también sugieren que no es difícil obtener una regla de divisibilidad para cualquier número $n$ superior a 10, que no sea múltiplo de 2 o de 5. El procedimiento es el siguiente:

Primero, debemos encontrar el menor entero positivo $s$ que sea múltiplo de $n$ y cuyo último dígito sea 9 o 18. 

Segundo, debemos calcular $s/10$ y redondear al entero más cercano. Al resultado lo llamaremos $q$.

Finalmente, formulamos esta regla: $N=\cba$ es divisible por $n$ si y solo si $P=\cb \pm q\times a$ es divisible por $n$. El signo de $q\times a$ en la fórmula para $P$ debe escogerse así: positivo si $s$ tiene 9 por último dígito, o negativo si el último dígito de $s$ es 1.

Sugerimos al lector interesado que se detenga a formular una regla de divisibilidad correspondiente para el 17 y que la utilice en un par de números apropiadamente seleccionados. El lector que haya llegado hasta aquí en esta discusión seguramente podrá luego formular la demostración rigurosa de que el procedimiento descrito siempre produce reglas de divisibilidad válidas (aunque muy poco útiles o eficientes). Quienes tengan interés en completar ese ejercicio pueden luego comparar su razonamiento con la demostración que damos a continuación.

La demostración que ofrecemos acá se aplica al caso en que $s=10q + 1$. (El caso $s=10q-1$ es muy similar y, para simplificar la discusión, no lo presentaremos aquí.)

Tenemos que $N=\cba$. Luego:

Y por lo tanto:

Por hipótesis, $s$ es divisible por $n$. Como $10$ y $n$ no comparten divisores, $N$ es divisible por $n$ si y solo si $P$ es divisible por $n$.

 
Inicio  1  2  3  4  5  6  7  8  9  10  11  12

 

Cidse - Revista virtual Matemática, Educación e Internet - ITCR
Derechos Reservados