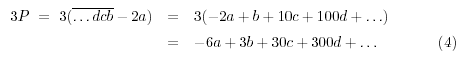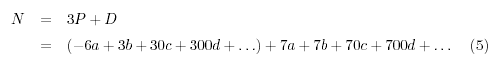Divisibilidad por 7

Un famoso "teorema'' reza que, de los enteros entre 0 y 100, todos los que parecen primos son primos, excepto el 91, que parece primo pero es igual a $7\times13$ ⁶. Evidentemente, 91 parece primo porque no tenemos un mecanismo sencillo para determinar cuándo un número es divisible por 7.

Seguramente muchos estudiantes a través de los siglos se habrán preguntado, al estudiar las reglas de divisibilidad básicas en el escuela o en el colegio, por qué no hay una regla de divisibilidad por 7. En realidad no es difícil formular una regla de divisibilidad por 7 o, como veremos, para cualquier otro entero que no sea múltiplo de 2 o de 5, pero estas reglas no son muy eficientes. Por este motivo tales reglas suelen no ser tan útiles como las que ya hemos discutido.

Una regla posible de divisibilidad por 7 es la siguiente: $N=\cba$ es divisible por 7 si y solo si $P=\cb -2a$ es divisible por 7. O sea, tomamos , eliminamos su último dígito y al número resultante le restamos 2 veces ese último dígito. es divisible por 7 si y solo ese nuevo número es divisible por 7. Por ejemplo, 91 es divisible por 7 porque $9-2\times1=7$ es divisible por 7. El entero 308 es divisible por 7 porque $30-2\times8=14$ es divisible por 7. La demostración de esta regla es la siguiente:

Tenemos que

Por lo tanto:

En la ecuación (5) hemos definido $D = 7a + 7b + 70c + 700d +\ldots$ , cantidad que evidentemente es siempre divisible por 7. Por lo tanto es divisible por 7 si y solo si es divisible por 7, y es divisible por 7 si y solo si es divisible por 7 ⁷.

Cada vez que aplicamos este proceso obtenemos un número que tiene solo uno o dos dígitos menos que el número que teníamos anteriormente. Claramente esta regla de divisibilidad es poco eficiente comparada con las reglas que mencionamos en el capítulo anterior.

Inicio 1 2 3 4 5 6 7 8 9 10 11 12

Cidse - Revista virtual Matemática, Educación e Internet - ITCR
Derechos Reservados