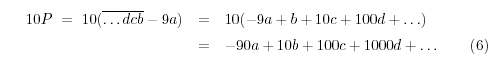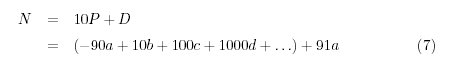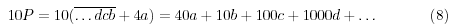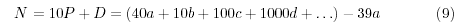|
Para el número 13 podemos formular esta regla: 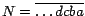 es divisible
por 13 si y solo si es divisible
por 13 si y solo si 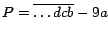 es divisible por 13. Por ejemplo, es divisible por 13. Por ejemplo, 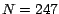 es divisible por 13 porque
es divisible por 13 porque
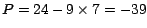 es divisible por 13. La
demostración de la validez de esta regla es la siguiente: es divisible por 13. La
demostración de la validez de esta regla es la siguiente:
Tenemos que:
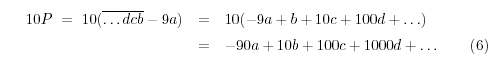
Por lo tanto:
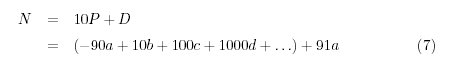
En la ecuación (7) hemos definido 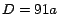 , cantidad
divisible por 13. , cantidad
divisible por 13. 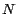 es, entonces, divisible por 13 si y solo si es, entonces, divisible por 13 si y solo si 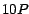 es divisible por 13 y, por lo tanto, también si y solo si
es divisible por 13 y, por lo tanto, también si y solo si 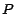 es
divisible por 13. es
divisible por 13.
Otra posible regla de divisibilidad por 13 que resulta en algunas
ocasiones más manejable es la siguiente: 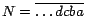 es divisible por 13
si y solo si es divisible por 13
si y solo si 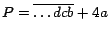 es divisible por 13. Por ejemplo, es divisible por 13. Por ejemplo, 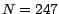 es
divisible por 13 porque es
divisible por 13 porque
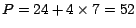 es divisible por 13 (si no lo
sabemos de antemano, podemos aplicar la regla nuevamente: es divisible por 13 (si no lo
sabemos de antemano, podemos aplicar la regla nuevamente:
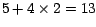 ). La demostración de la validez de esta regla es la
siguiente: ). La demostración de la validez de esta regla es la
siguiente:
Tenemos que:
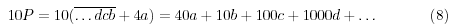
Por lo tanto:
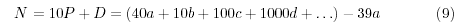
En la ecuación (9) hemos definido 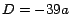 , cantidad
divisible por 13. , cantidad
divisible por 13. 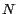 es, entonces, divisible por 13 si y solo si es, entonces, divisible por 13 si y solo si 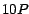 es divisible por 13, y por lo tanto también si y solo si
es divisible por 13, y por lo tanto también si y solo si 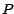 es
divisible por 13. es
divisible por 13.
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|