1 2 3 4 5 6 7 8 9 10 11 12

 

Redes de transporte

Una red de transporte es una herramienta que nos permite modelar problemas sobre flujo de materiales. Imagine, por ejemplo, un producto navegando a través de un sistema desde una fuente, en donde el material es producido, hasta un destino, en donde es consumido o almacenado. La fuente produce el material y es capaz de bombearlo a una cierta velocidad fija, de suerte que los destinatarios pueden consumirlo o almacenarlo a la misma velocidad. Intuitivamente podemos pensar que el "flujo" del material en cualquier punto del sistema es la velocidad a la cual el material se mueve. De esta forma las redes de transporte pueden ser usadas para modelar líquido fluyendo a través de tuberías, partes a través de líneas de ensamblaje, corriente a través de redes eléctricas, información a través de redes de comunicación, etc. El problema de flujo máximo en redes de transporte se refiere a la consecución de la tasa o velocidad máxima a la cual el material puede ser bombeado de la fuente al destino sin violar las capacidades de los conductos intermedios. 

Definición
Una red de transporte (o simplemente red) es un digrafo $ G=(V, E) $ simple (i.e. sin lazos o rizos ni lados paralelos), con las siguientes propiedades:

  • Existe un solo nodo en $ G $, que solo tiene lados de salida y no tiene lados de llegada; tal nodo se denomina la fuente.

  • Existe un solo vértice en $ G $, que solo tiene lados de entrada y no tiene lados de salida; tal nodo se denomina el depósito o destino.

  • Para cada lado $ e =(i, j) $ que une digamos, los vértices $ v_i $ y $ v_j $ se asocia un número real $ C_{ij}\geq 0 $, que se conoce como la capacidad de la arista $ e $. Formalizando un poco más este concepto, podemos pensar que existe una función de valor real $\displaystyle C:V\times V\mapsto [0, \, +\infty [ $, tal que si el par $ (a, b)\not\in E $, entonces $ C_{a, b} = C(a, b) :=0 $. Dicha función se llama la función capacidad

  • Para cualquier vértice $ v $ en $ G $, existirá al menos un lado de entrada o un lado de salida.

No se debe confundir los conceptos de capacidad (que acabamos de definir) y flujo (que es la próxima definición), el hecho de que una tubería tenga capacidad 50, no quiere decir que ese será el flujo que transportará.

Definición
Sea $ G $ una red de transporte, y $ C_{ij} $ la capacidad de la arista (dirigida) $ e =(i, j) $, definimos el flujo en la arista $ e $ como una cantidad real $ F_{ij}\geq 0 $ que satisface las siguientes características:

  • (RESTRICCIÓN DE CAPACIDAD) El flujo no supera la capacidad en cada lado, i.e. $\displaystyle F_{ij}\leq C_{ij} $.

  • (FLUJO NULO) Si entre el vértice $ i $ y el vértice $ j $ no hay arista, se define $ F_{ij} = 0 $.

  • (CONSERVACIÓN DEL FLUJO) La cantidad de flujo que entra a un nodo (que no es ni fuente ni destino) es la misma cantidad que sale de él. Más detalladamente, para cada nodo $ j $, que no es ni fuente ni depósito, se cumple

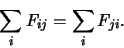
    \begin{displaymath} \sum_ iF_{ij} = \sum_{i} F_{ji}. \end{displaymath}

Formalizando un poco más el concepto de flujo podemos pensar de éste como una función $\displaystyle F: V\times V \mapsto [0, \, +\infty [ $ tal que $ i $ y $ j $ son vértices de $ G $, entonces $\displaystyle F(i, j) = F_{ij} $.

 

Figura 1.1: $ F $: Fuente, $ D $: Destino.
\begin{figure}\begin{center} \unitlength=1.50mm \linethickness{0.4pt} \begin{... ...makebox(0,0)[cc]{50/1}} \end{picture} \end{center}\vspace{-4em} \end{figure}

 

En la Fig.1.1 utilizamos la notación $ c $ /$ f $ para indicar que la arista con capacidad $ c $ está transportando $ f $ unidades de flujo. Note que al nodo $ v_3 $ llegan 4 unidades de flujo y salen 4 unidades de flujo. Esto ilustra la propiedad de la conservación del flujo. Observe también que de la fuente salen 9 unidades de flujo y al depósito llegan 9 unidades de flujo. Esta propiedad se cumple siempre, y la registramos en el siguiente teorema. Teorema
Sea $ F $ un flujo sobre una red $ G $, entonces se cumple que el flujo que sale de la fuente es igual al flujo que llega al depósito; más exactamente

\begin{displaymath} \sum_i F_{fi} = \sum_i F_{id}, \end{displaymath}

en donde $ f $ es el nodo fuente y $ d $ es el nodo destino.

 


DEMOSTRACIÓN: El lector puede encontrar la demostración en [8]. $ \Box $

 1 2 3 4 5 6 7 8 9 10 11 12

Revista Virtual, Matemática Educación e Internet.
Derechos Reservados.