El método de Ford-Fulkerson
Para una red de transporte
, estamos interesados en obtener la forma de utilizar optimamente las "tuberías" de las que se dispone, dicho de otra forma queremos obtener la mayor cantidad de flujo que se pueda transportar por la red sin violar las capacidades predefinidas. El método de Ford-Fulkerson resuelve el problema del flujo máximo. Le llamamos método y no un "algoritmo" dado que permite varias implementaciones con diferentes tiempos de ejecución (para un estudio sobre tiempos de ejecución se sugiere consultar [1,4]). El método Ford-Fulkerson es iterativo, puesto que se empieza con un flujo nulo (soportado por las tuberías de la red) y luego éste se va aumentando hasta que logre el mayor flujo posible sin violar las restricciones de capacidad. Para lograr ir aumentando la cantidad de flujo transportado, en cada paso utilizaremos el concepto de ruta aumentante o semivía, la cual puede pensarse como un camino desde la fuente hasta el destino por el que se puede empujar o mandar todavía flujo. El método de Ford-Fulkerson consiste en utilizar tantas rutas aumentantes como existan. En [5], el método de Ford-Fulkerson se resume de la siguiente forma:
Método Ford-Fulkerson
- Inicie el flujo
en 0.
- WHILE exista una ruta aumentante
DO
- Aumente el flujo
a lo largo de
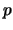
- RETURN
.
Dicho en otras palabras, la idea es encontrar conductos subutilizados entre la fuente y el destino, que pueden aumentarse hasta que una restricción de capacidad detenga el aumento. En varios textos se consiguen implementaciones más o menos detalladas del método de Ford-Fulkerson, consulte la presentada en [10] (también puede consultar [5]).