| Walter Mora F. | Revista Digital Matemática, Educación e Internet |

 

1 2 3 4 5 6 7 8 9 10

 

Introducción

Si $ x$ es una variable, expresiones como

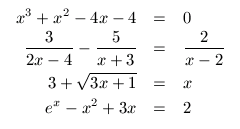
se denominan ecuaciones en $ x$. Por otro lado, dada cualquier ecuación en $ x$, si al sustituir a $ x$ con un número $ a$ se obtiene un enunciado verdadero, entonces $ a$ se llama solución o raíz de la ecuación $ f(x)=0$. También es común decir que $ a$ satisface la ecuación. Por ejemplo, $ a=\frac{5}{12}$ es una solución de la ecuación

$\displaystyle \left(8x-2 \right) \left(3x+4 \right) = \left(4x+3 \right) \left( 6x-1 \right) $

ya que al sustituir $ x$ por $ \frac{5}{12}$ obtenemos


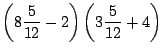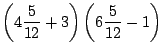$\displaystyle \left(8 \frac{5}{12} -2 \right) \left(3 \frac{5}{12} +4 \right)$ $\displaystyle =$ $\displaystyle \left(4 \frac{5}{12} + 3 \right) \left( 6 \frac{5}{12} -1 \right)$
$\displaystyle \frac{4}{3} \cdot \frac{21}{4}$
 $\displaystyle =$ $\displaystyle \frac{14}{3} \cdot \frac{3}{2}$
$\displaystyle 7$ $\displaystyle =$ $\displaystyle 7,$

que es una proposición verdadera. Resolver una ecuación significa hallar todas sus soluciones.

Si todo número en el dominio de la variable $ x$ es una solución de una ecuación dada, a esta ecuación se le llama identidad. Por ejemplo,

$\displaystyle \left(x-7 \right)^2 - 4= \left(x-9 \right)\left(x-5 \right) $

es una identidad, puesto que se convierte en una proposición verdadera para todos los números del dominio de $ x$, en este caso    $ \mbox{$I \hspace{-1.3mm} R$}$$ $.

El hecho de que una ecuación tenga o no solución depende del sistema de números que consideremos como recorrido para la variable $ x$. Por ejemplo, si pedimos que las soluciones sean números enteros, entonces la ecuación $ 2x=5$ no tiene solución, ya que no existe ningún entero tal que su duplo sea 5. Sin embargo, si aceptamos soluciones racionales, entonces $ \frac{5}{2}$ es la solución buscada. De igual manera, la ecuación $ x^2=2$ no tiene soluciones racionales; pero sí soluciones reales: $ \pm \sqrt{2}$.

Se dice que dos ecuaciones son equivalentes si tienen las mismas soluciones. Por ejemplo, las ecuaciones   



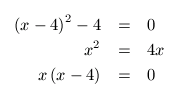
son equivalentes.

Esto da origen al método más usado para resolver ecuaciones, el cual consiste en generar una sucesión de ecuaciones equivalentes, cada una de las cuales es de algún modo más sencilla que la anterior, hasta llegar a una ecuación cuyas soluciones son obvias. Por lo general, esta sucesión de ecuaciones equivalentes se logra usando propiedades de los números reales, tales como: sumar o restar la misma expresión a ambos lados de la ecuación, multiplicar o dividir a ambos lados de la ecuación por una expresión diferente de cero, elevar al cuadrado a ambos lados de la ecuación, etc. El siguiente ejemplo ilustra este proceso.


$\displaystyle 5x - 3$ $\displaystyle =$ $\displaystyle 2x + 1$  
$\displaystyle \left(5x - 3 \right) + 3$ $\displaystyle =$ $\displaystyle \left(2x + 1 \right) + 3$  
$\displaystyle 5x$ $\displaystyle =$ $\displaystyle 2x + 4$  
$\displaystyle 5x - 2x$ $\displaystyle =$ $\displaystyle \left(2x + 4 \right) - 2x$  
$\displaystyle 3x$ $\displaystyle =$ $\displaystyle 4$  
$\displaystyle \frac{1}{3} 3x$ $\displaystyle =$ $\displaystyle \frac{1}{3} 4$  
$\displaystyle x$ $\displaystyle =$ $\displaystyle \frac{4}{3}$  

Durante el proceso de reducción podemos, por ejemplo, multiplicar por una expresión que se anula para algún valor de $ x$, o tomar el cuadrado a ambos lados de la ecuación, estas operaciones pueden producir ecuaciones que no son equivalente. Veamos un ejemplo.


$\displaystyle 2x -3$ $\displaystyle =$ $\displaystyle \sqrt{x+6}$
$\displaystyle \left(2x-3 \right)^2$ $\displaystyle =$ $\displaystyle \left( \sqrt{x+6} \right)^2$
$\displaystyle 4x^2 - 12x + 9$ $\displaystyle =$ $\displaystyle x + 6$
$\displaystyle 4x^2 - 13x + 3$ $\displaystyle =$ 0

De donde obtenemos que $ x=3$ y $ x=\frac{1}{4}$, pero al sustituir $ x$ por $ \frac{1}{4}$ en la ecuación original obtenemos


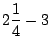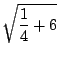$\displaystyle 2 \frac{1}{4} - 3$ $\displaystyle =$ $\displaystyle \sqrt{\frac{1}{4} + 6}$  
$\displaystyle - \frac{5}{2}$ $\displaystyle =$ $\displaystyle \sqrt{ \frac{25}{4} }$  
$\displaystyle - \frac{5}{2}$ $\displaystyle =$ $\displaystyle \frac{5}{4}$  

Con lo cual $ \frac{1}{4}$ no es solución. Cualquier solución de la nueva ecuación que no es solución de la ecuación original se llama solución extraña.

Lo que ha sucedido, en este caso, es que al tomar el cuadrado a ambos lados de la ecuación hemos obtenido una ecuación que no es equivalente con la anterior, y por tanto, algunas soluciones de la última ecuación podrían no serlo de la ecuación original.

Una ecuación de la forma

$\displaystyle p(x) = a_nx^n + a_{n-1} x^{n-1} + \ldots + a_1x + a_0 = 0 $

donde cada $ a_i \in$   $ \mbox{$I \hspace{-1.3mm} R$}$$ $ y $ a_n \neq 0$; se llama ecuación polinomial. Recuerde que si $ p(a)=0$, entonces decimos que $ a$ es un cero del polinomio $ p(x)$, o bien, $ a$ es una solución o raíz de la ecuación $ p(x)=0$.

A excepción de casos especiales, resulta muy difícil encontrar las raíces de una ecuación polinomial. Por ejemplo, no son evidentes las raíces de la ecuación polinomial

$\displaystyle x^5 - 3x^4 + 4x^3 + 4x - 10 = 0 $

Aún más, no existe una fórmula que pueda usarse para encontrar tales raíces.

Como vemos, buscar las soluciones de una ecuación $ f(x)=0$, no es en general una tarea fácil, ni aún cuando $ f(x)$ es un polinomio y ni hablar de cuando la ecuación involucra funciones trascendentes1.

A excepción de los casos triviales, podríamos decir que las únicas ecuaciones $ f(x)=0$ que podemos resolver de forma exacta, son aquellas para las cuales $ f(x)$ es un polinomio de grado menor o igual a 3, claro está, después del proceso de reducción.

Por está razón, necesitamos métodos que nos permitan, no digamos hallar, sino más bien aproximar las soluciones de una ecuación dada. Este tipo de métodos cae dentro de un área de la matemática que se conoce como Análisis Numérico.

 

1 2 3 4 5 6 7 8 9 10

Revista digital Matemática, Educación e Internet.
Derechos Reservados