| Walter Mora F. | Revista Digital Matemática, Educación e Internet |

 

1 2 3 4 5 6 7 8 9 10

 

Método de la bisección

 

Esta técnica se basa en el teorema del valor intermedio y parte del supuesto que $ f(a)$ y $ f(b)$ tienen signos opuestos. Aunque el procedimiento funciona bien para el caso en el que existe más de una solución en el intervalo $ ]a,b[$ , se considera por simplicidad que es única la raíz en dicho intervalo.

Básicamente, el método consiste en dividir a la mitad repetidamente los subintervalos de $ [a,b]$ y en cada paso, localizar la mitad que contiene a la solución, $ m$.

Para empezar, hacemos $ a_1=a$ y $ b_1=b$ y calculamos el punto medio del intervalo $ [a_1,b_1]$ y lo llamamos

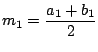
$\displaystyle m_1 = \frac{a_1 + b_1}{2} $

Si $ f(m_1)=0$, entonces $ m=m_1$ ; si no, $ f(m_1)$ tiene el mismo signo que $ f(a_1)$ o $ f(b_1)$. Si $ f(m_1)$ y $ f(a_1)$ tienen el mismo signo, entonces $ m \in ]m_1,b_1[$, y tomanos $ a_2=m_1$ y $ b_2=b_1$. Si $ f(m_1)$ y $ f(b_1)$ tienen el mismo signo, entonces $ m \in ]a_1,m_1[$, y tomanos $ a_2=a_1$ y $ b_2=m_1$. Luego repetimos este proceso al intervalo $ [a_2,b_2]$. Esto produce el método descrito en el algoritmo de la figura 3.

Figura 3: Algoritmo de la bisección.
\begin{figure} \begin{tabbing} \hspace*{1.7in}\=\hspace*{0.25in}\=\hspace*{0.2... ...} \\ \> $m:=m_1$\ \\ \> \texttt{End} \\ \> \end{tabbing} \end{figure}

 

Observación: como en cada iteración el intervalo es la mitad del intervalo anterior, podemos concluir que en la iteración $ n$ la solución $ m$ se encuentra en un intervalo de longitud

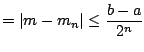
   Error Absoluto$\displaystyle = \left\vert m - m_n \right\vert \leq \frac{b-a}{2^n} $

para $ n \geq 1$. Esto nos permite tener una idea de que tan cerca estamos de la solución real, incluso podemos usar esto para estimar el número de iteraciones necesarias para alcanzar una presición dada.

La implementación de este algoritmo con Excel es muy sencillas, como veremos.

Ejemplo


Para ilustar la forma en que podemos usar Excel, vamos a aproximar la solución de la ecuación

$\displaystyle x^3 +4x^2 -10 = 0 $

Lo primero es hallar un intervalo en el cual podamos garantizar la existencia de una solución. Por el teorema de las cotas sabemos que esta ecuación tiene sus soluciones dentro del intervalo $ [-5,2]$. Ahora, podemos usar el teorema del valor intermedio para refinar el intervalo a $ [1,\frac{1}{2}]$ y el teorema de Sturm para garantizar la unicidad de la solución real ([Childs 1995], [Kurosch 1987]). El próximo paso es usar Excel.

 

  1. En las celdas A4 y B4 escribimos los valores de $ a=1$ y $ b=\frac{1}{2}$, respectivamente.

  2. En la celda C4 escribimos la fórmula que calculará los puntos medios del intervalo:

    $\displaystyle {\tt =promedio(A4;B4)}. $

  3. En la celda D4 escribimos la fórmula que calculará $ f(a_i)$:

    $\displaystyle {\tt =potencia(A4;3)+4*potencia(A4;2)-10}. $

  4. En la celda E4 escribimos la fórmula que calculará $ f(b_i)$:

    $\displaystyle {\tt =potencia(B4;3)+4*potencia(B4;2)-10}. $

  5. En la celda F4 escribimos la fórmula que calculará $ f(m_i)$:

    $\displaystyle {\tt =potencia(C4;3)+4*potencia(C4;2)-10}. $

  6. En la celda G4 escribimos la fórmula que calculará el error

    $\displaystyle {\tt (B4-A4)/2}. $

  7. En la celda A5 escribimos la fórmula que calculará el nuevo extremo $ a_i$:

    $\displaystyle {\tt SI(E4*F4<0;C4;A4)}. $

  8. En la celda B5 escribimos la fórmula que calculará el nuevo extremo $ b_i$:

    $\displaystyle {\tt SI(D4*F4<0;C4;B4)}. $

 

Y por último, lo único que debemos hacer es ir generando las aproximaciones, para esto arrastramos cada columna una a una. El resultado de esto se muestra en la figura 4.

 
Figura 4: Método de la bisección: $ x^3+4x^2-10=0$

El método de la bisección, aunque es conceptualmente claro, tiene inconvenientes importantes. Es muy lento en su convergencia (es decir, $ n$ tiene que ser muy grande para que $ \left\vert m-m_n \right\vert$ sea pequeño, por ejemplo, se requiere de $ 10$ iteraciones para obtener un error absoluto menor a $ 10^{-3}$ en el ejemplo anterior), además una buena aproximación intermedia puede ser descartada inadvertidamente. Sin embargo, el método tiene la importante propiedad de que siempre converge a una solución, además de que lo único que se requiere es que $ f$ sea continua, es por estas razones que se usa con frecuencia como punto de partida de métodos más eficientes.

 

1 2 3 4 5 6 7 8 9 10

Revista digital Matemática, Educación e Internet.
Derechos Reservados