| Walter Mora F. | Revista Digital Matemática, Educación e Internet |

 

 

1 2 3 4 5 6 7 8 9 10

 

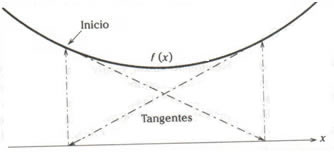
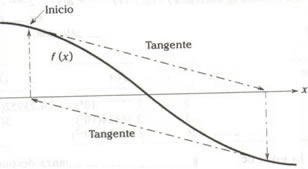
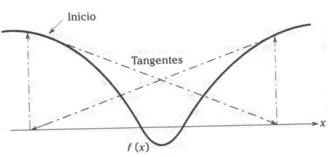
Sin embargo, algunas veces el método de Newton no converge, sino que se encicla. Esto puede ocurrir, por ejemplo, si no hay raíz real, si la raíz es un punto de inflexión o si la aproximación inicial está muy lejos de la raíz buscada y el proceso de aproximación cae en un ciclo. Estas situaciones se ilustran en la figura 7a, 7b, 7c.

Figura 7a: Oscilaciones para una función sin raíz real.

 

Figura 7b: Oscilaciones para una función con punto de inflexiónl.

 

Figura 7c: Oscilaciones para una función con dos raíces reales.

 

En la figura 8 se muestra una situación en la que no hay convergencia. Se está tratando de aproximar la solución de la ecuación polinomial

$$10x^3-8.3x^2+2.295x-0.21141=0$$

con una aproximación inicial de $0.28$. Obsérvese que en este caso las aproximaciones van creciendo y se alejan cada vez más de la verdadera solución $0.29$. Para este ejemplo lo que sucede es que una de las aproximaciones $x_1=0.27$ es solución de la ecuación $f^{\prime}(x)=0$.

Otra de las desventajas potenciales del método de Newton es que requiere de la evaluación de la primera derivada de $f(x)$. Para la mayoría de los problemas de los textos este requisito es trivial, pero éste no es el caso en problemas reales donde, por ejemplo, la función $f(x)$ podría estar dada en forma tabular.

Figura 8: Situación donde no hay convergencia, usando Excel.

 

Con el propósito de evitar esta desventaja, podemos sustituir la derivada por una interpolación lineal, es decir, podemos usar el hecho de que

$$f^{\prime}(x_n) \approx \frac{f(x_{n+1}) - f(x_n) }{x_{n+1} - x_n}$$

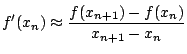
Con lo cual la fórmula recursiva del método de Newton se reduce a

$$x_{n+1} = x_n - \frac{\left(x_{n+1} - x_{n} \right)f(x_n)}{f(x_{n+1}) - f(x_n)}$$

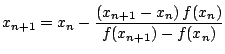
para $n \geq 2$.

Esta pequeña variante da origen a un método conocido como el método de la secante, el cual necesita de dos aproximaciones iniciales. En la figura 9 se muestran los resultados obtenidos con este método.

Figura 9: Método de la secante.

 

1 2 3 4 5 6 7 8 9 10

Revista digital Matemática, Educación e Internet.
Derechos Reservados