| Walter Mora F. | Revista Digital Matemática, Educación e Internet |

 

1 2 3 4 5 6 7 8 9 10

 

Métodos para la aproximación de soluciones

La mayoría de las veces la solución de un problema real conduce a la elaboración de un modelo matemático, modelo que esperamos conduzca a soluciones con sentido físico. Si los modelos son sencillos, las soluciones se pueden obtener con las técnicas matemáticas normales. Sin embargo, en algunos casos es necesario recurrir a técnicas numéricas que involucran muchos cálculos y es aquí donde una herramienta como Excel puede ser de mucha utilidad.

Por ejemplo, bajo ciertas condiciones la posición $ x$ de un objeto de masa $ m$ que cae bajo la influencia de la gravedad, con una velocidad inicial $ v_0$ puede ser modelada por el siguiente problema de valor inicial


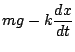$\displaystyle m \frac{d^2x}{dt}$ $\displaystyle =$ $\displaystyle mg - k \frac{dx}{dt}$
$\displaystyle x(0)$ $\displaystyle =$ 0
$\displaystyle x^{\prime}(0)$ $\displaystyle =$ $\displaystyle v_0$

donde $ g$ es la gravedad y $ k$ la constante de resistencia, debida al aire.

La solución de este problema está dada por

$\displaystyle x(t) = \frac{mg}{k}t + \frac{m}{k} \left(v_0 - \frac{mg}{k} \right) \left( 1 - e^{-kt/m} \right) $

Ahora, suponga que el objeto tiene una masa $ 3 kg$ y se deja caer bajo la influencia de la gravedad de una altura de 10 m sobre el nivel del suelo. Suponiendo que la fuerza gravitacional es constante ( $ 9.81 m/seg^2$) y que la fuerza de resistencia debida al aire es proporcional a la velocidad del objeto, con constante de proporcionalidad de $ 3 kg/seg$. Entonces, si quisiéramos determinar el momento justo en el que el objeto golpea contra el suelo necesitariamos despejar $ t$ de la siguiente ecuación

$\displaystyle t + e^{-t} = 2.02 $

Pero desafortunadamente, para esta ecuación no es posible despejar explícitamente $ t$. Los métodos numéricos que vamos a analizar nos permitirán resolver mediante aproximaciones ecuaciones de este tipo.

Nuestro objetivo será mostrar como podemos usar Excel para resolver numéricamente ecuaciones y no el análisis teórico de los métodos numéricos involucrados, para esto recomendamos al lector consultar [Acton, 1990], [Akai, 1999], [Burden, 1996], [Nieves, 1998] o [Ralston, 1986].


Subsecciones

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados