| Walter Mora F. | Revista Digital Matemática, Educación e Internet |
 

1 2 3 4 5 6 7 8 9 10

 

Método de punto fijo

 

Un punto fijo de una función $ g$, es un número $ p$ tal que $ g(p)=p$. El problema de encontrar las soluciones de una ecuación $ f(x)=0$ y el de encontrar los puntos fijos de una función $ h(x)$ son equivalentes en el siguiente sentido: dado el problema de encontar las soluciones de una ecuación $ f(x)=0$, podemos definir una función $ g$ con un punto fijo $ p$ de muchas formas; por ejemplo, $ f(x)=x - g(x)$. En forma inversa, si la función $ g$ tiene un punto fijo en $ p$, entonces la función definida por $ f(x)=x - g(x)$ posee un cero en $ p$.

El método de punto fijo inicia con una aproximación inicial $ x_0$ y $ x_{i+1} = g(x_i)$ genera una sucesión de aproximaciones la cual converge a la solución de la ecuación $ f(x)=0$. A la función $ g$ se le conoce como función iteradora. Se puede demostrar que dicha sucesión $ \langle x_n \rangle$ converge siempre y cuando $ \left\vert g^{\prime}(x) \right\vert <1$.

Ejemplo
Usando el método de punto fijo vamos a aproximar la solución de la ecuación $ x^3+4x^2-10=0$ dentro del intervalo $ [1,2]$.

Lo primero es buscar una función $ g(x)$ adecuada


$\displaystyle x^3 + 4x^2 - 10$ $\displaystyle =$ 0  
$\displaystyle x^2 \left(x + 4 \right)$ $\displaystyle =$ $\displaystyle 10$  
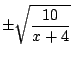$\displaystyle x$ $\displaystyle =$ $\displaystyle \pm \sqrt{\frac{10}{x+4}}$  

Y claramente elegimos como función iteradora a

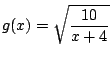
$\displaystyle g(x) = \sqrt{\frac{10}{x+4}} $

además observe que

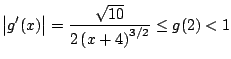
$\displaystyle \bigr\vert g^{\prime}(x) \bigr\vert = \frac{\sqrt{10}}{2\left( x +4 \right)^{3/2}} \leq g(2) < 1 $

para toda $ x \in [1,2]$, lo cual garantiza que la sucesión que vamos a construir va a ser convergente.

La implementación de este método en Excel es realmente simple, como veremos.

 

  1. En la celda A5 escribimos nuestra aproximación inicial, en este caso 2.

  2. En la celda A6 escribimos la fórmula que calculará las aproximaciones:

    $\displaystyle {\tt =raiz(10/(A5+4))}. $

  3. Por último arrastramos la celda A6 para generar las restantes aproximaciones.

En la figura 10 se muestran los resultados generados por este método.

Figura 10: Iteración de punto fijo.

 

Una desventaja potencial del método de punto fijo es que la elección de la función iteradora $ g(x)$ no siempre es fácil.

En esta pequeña nota no hemos pretendido ser exhaustivos en la teoría ligada a los métodos numéricos expuestos, pues para esto existen muchos libros de análisis numérico que podrían consultarse ([Acton, 1990],[Akai, 1999],[Burden, 1996],, [Nieves, 1998]), la idea ha sido introducir de una forma básica el uso de Excel para la aproximación de soluciones de ecuaciones. La implementación de los métodos expuestos pueden ser mejorados con la ayuda de macros, tema que esperamos tratar en algún momento. Por lo pronto ha sido todo y hasta la próxima entrega.

1 2 3 4 5 6 7 8 9 10

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados