
|
Este es uno de los métodos más eficientes para aproximar las soluciones de
la ecuación ![]() . El método de Newton empieza con una aproximación inicial
. El método de Newton empieza con una aproximación inicial ![]() , la siguiente aproximación
, la siguiente aproximación ![]() corresponde a la intersección con el eje
corresponde a la intersección con el eje ![]() de la recta tangente a la gráfica de
de la recta tangente a la gráfica de ![]() en
en
![]() . La aproximación
. La aproximación ![]() corresponde a la intersección con el eje
corresponde a la intersección con el eje ![]() de la tangente a la gráfica de
de la tangente a la gráfica de ![]() en el punto
en el punto
![]() , y así sucesivamente. Este proceso genera una sucesión
, y así sucesivamente. Este proceso genera una sucesión
![]() , definida por
, definida por
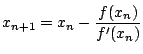
para ![]() .
.
El algoritmo del método se muestra en la figura 5
La implementación de este método, en Excel, es realmente simple. Para
esto considere la mismo ecuación de antes:
![]() y con aproximación inicial tomenos
y con aproximación inicial tomenos ![]() .
.
|
El resultado de este proceso se muestra en la figura 6.
Observe la gráfica de la función
![]() , las rectas tangentes a
, las rectas tangentes a ![]() en
en ![]() y
y ![]() respectivamente y las dos aproximaciones generadas por estas aproximaciones.
respectivamente y las dos aproximaciones generadas por estas aproximaciones.
|
Figura 6: Método de la Newton aplicado
a
|
Cuando el método de Newton converge se obtienen los resultados con relativa
rapidez, ya que para raíces no repetidas este método converge con orden 2, y
el error es proporcional al cuadrado del error anterior, es decir, si el error
![]() , el siguiente error
, el siguiente error
![]() es proporcional a
es proporcional a ![]() y así sucesivamente. Con lo que podríamos decir que en cada
iteración aproximadamente se duplica el número de dígitos correctos.
y así sucesivamente. Con lo que podríamos decir que en cada
iteración aproximadamente se duplica el número de dígitos correctos.
Revista digital Matemática, Educación e Internet.
Derechos Reservados