| 1 2
3 4
5 6 7
8 9
``Diremos que un número real no negativo 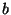 es una longitud constructible si, mediante un número finito
de aplicaciones de la regla y el compás y los puntos de intersección
obtenidos entre rectas y círculos así construídos, se puede
construir un segmento de recta de longitud es una longitud constructible si, mediante un número finito
de aplicaciones de la regla y el compás y los puntos de intersección
obtenidos entre rectas y círculos así construídos, se puede
construir un segmento de recta de longitud 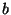 '' (Herstein,1988) '' (Herstein,1988)
Algunas de las construcciones que se pueden realizar son las siguientes:
- Cualquier longitud que se construya sobre una recta se puede transportar
a otra recta mediante el compás y por tanto es constructible en
la segunda recta.
- Podemos trazar una recta paralela a una recta dada que pase por un
punto dado.
- Se puede construir una longitud
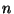 para cualquier entero no negativo para cualquier entero no negativo 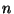 . .
De estos resultados se logra construir cualquier longitud racional 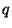 . .
Para extender la noción de constructibilidad a números negativos
enunciaremos la siguiente definici˛n:
Un número real 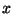 es un número constructible si es un número constructible si 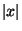 es una longitud constructible es una longitud constructible
Así llegamos a nuestro primer resultado interesante. Los resultados
enunciados nos permiten demostrar que el conjunto de números reales
constructibles 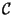 junto con las operaciones usuales de junto con las operaciones usuales de
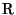 forman un subcampo del campo de los números
reales forman un subcampo del campo de los números
reales
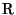 . Este subcampo contiene al conjunto de los números
racionales . Este subcampo contiene al conjunto de los números
racionales
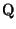 pero esta inclusión es propia pues ya sabemos
que pero esta inclusión es propia pues ya sabemos
que 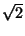 es fácilmente constructible con regla y compás. es fácilmente constructible con regla y compás.
1 2
3 4
5 6 7
8 9
|

