| 1 2
3 4
5
6 7 8 9
El último criterio enunciado nos permite resolver como un corolario
los problemas que tuvieron desvelados a los matemáticos por más
de dos mil años. En efecto:
- No se puede cuadrar un círculo: Para construir un cuadrado
de área igual a un circulo de radio 1 , usando regla y compás,
se debe poder construir el número
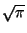 . Como se vio en los ejemplos anteriores, Lindeman demostró
que . Como se vio en los ejemplos anteriores, Lindeman demostró
que 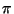 es tracendente sobre es tracendente sobre
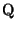 . Luego, . Luego, 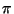 no puede ser la raíz de ningún polinomio con coeficientes
en no puede ser la raíz de ningún polinomio con coeficientes
en
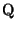 . Esto dice que no existe un polinomio minimal para . Esto dice que no existe un polinomio minimal para
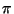 sobre sobre
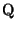 . En consecuencia, . En consecuencia, 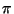 no puede ser constructible y como vimos que los números constructibles
forman un subcampo de los
números reales, se tiene que no puede ser constructible y como vimos que los números constructibles
forman un subcampo de los
números reales, se tiene que 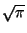 tampoco puede ser constructible. tampoco puede ser constructible.
- No se puede duplicar el Cubo: Razonando por contradicción
se tiene que si se pudiese duplicar un cubo de lado 1, se necesitaría
construir con regla y compás un cubo cuya arista midiera
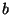 y cuyo volúmen fuera 2. Dado que el volumen del cubo sería y cuyo volúmen fuera 2. Dado que el volumen del cubo sería
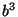 , se debe poder construir un numero , se debe poder construir un numero 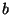 tal que tal que 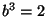 . Esto dice que . Esto dice que 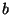 debe ser raíz del polinomio debe ser raíz del polinomio 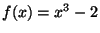 . Como este polinomio es mónico e irreducible sobre . Como este polinomio es mónico e irreducible sobre
 (por el teorema de raíces racionales), se concluye que es el
polinomio minimal de (por el teorema de raíces racionales), se concluye que es el
polinomio minimal de 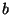 en en
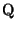 , pero esto nos produce una contradicción ya que
el grado de , pero esto nos produce una contradicción ya que
el grado de 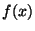 es 3 y no es una potencia de 2 contradiciendo el criterio de constructibilidad
mencionado. es 3 y no es una potencia de 2 contradiciendo el criterio de constructibilidad
mencionado.
- No se puede trisecar un ángulo: De nuevo razonamos por
contradicción. Si se pudiera trisecar un ángulo cualquiera,
el ángulo de
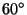 debe de poderse trisecar. Esto dice que se podría construir
un triángulo rectángulo debe de poderse trisecar. Esto dice que se podría construir
un triángulo rectángulo 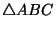 tal que tal que
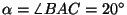 y y
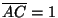 . .
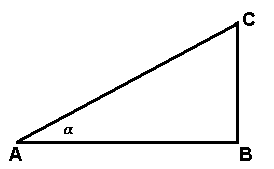
Como
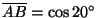 , se tendría que , se tendría que
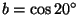 es tambien constructible. Por otro lado, la identidad
trigonométrica del ángulo triple es tambien constructible. Por otro lado, la identidad
trigonométrica del ángulo triple
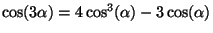 para el caso en que para el caso en que
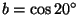 indica que indica que
de donde
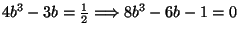 . Haciendo el cambio de
variable . Haciendo el cambio de
variable 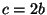 , se llega a la ecuación , se llega a la ecuación 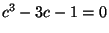 . Como los números constructibles son un campo, si . Como los números constructibles son un campo, si 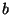 es constructible entonces es constructible entonces 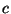 también lo es. Pero si también lo es. Pero si 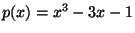 entonces entonces 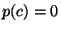 y como y como 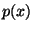 es mónico e irreducible sobre es mónico e irreducible sobre
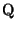 , se tiene que , se tiene que 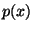 es el polinomio minimal de es el polinomio minimal de 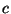 sobre sobre
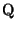 . Como el grado de . Como el grado de 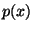 es 3 se tiene que es 3 se tiene que 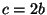 no es constructible y esto es una contradicción. Por tanto
hemos encontrado un contraejemplo y en consecuencia, no se pueden trisecar
ángulos. no es constructible y esto es una contradicción. Por tanto
hemos encontrado un contraejemplo y en consecuencia, no se pueden trisecar
ángulos.
1 2
3 4
5
6 7 8 9
|

