| 1 2
3 4
5 6 7
8 9
Evariste Galois, un matemático francés del siglo XVIII desarrolló
la teoría que lleva su nombre. Cuenta la historia que la noche antes
de morir escribió una carta en la que se desarrolla esta teoría.
Con esta teoría se logran fundir de una manera brillante el álgebra
y la geometría.
Primero recordaremos algunas definiciones importantes:
Sea 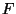 un campo. Un polinomio con coeficientes en F en la incógnita un campo. Un polinomio con coeficientes en F en la incógnita
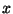 se llama reducible en se llama reducible en 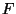 si es producto de otros dos polinomios con coeficientes en F de grado
menor. Si un polinimio no es reducible se dice irreducible . si es producto de otros dos polinomios con coeficientes en F de grado
menor. Si un polinimio no es reducible se dice irreducible .
El polinomio 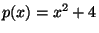 es irreducible o no factorizable sobre es irreducible o no factorizable sobre
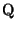 en tanto que el polinomio en tanto que el polinomio
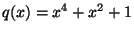 es reducible en es reducible en
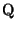 ya que ya que
Sea 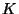 un campo y sea un campo y sea 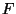 un subcampo de un subcampo de 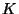 . Decimos que . Decimos que 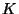 es una extensión de es una extensión de 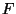 . .
Si 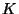 es un campo y es un campo y 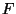 un subcampo de un subcampo de 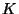 y si y si
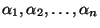 son elementos de son elementos de 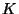 , llamaremos a , llamaremos a
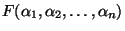 el cuerpo obtenido con la adjunción
de los elementos el cuerpo obtenido con la adjunción
de los elementos
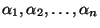 de de 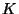 . .
El campo
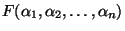 es la mínima extensión
de es la mínima extensión
de 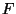 que contiene a que contiene a
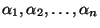 . .
Un caso partricular de esta situación se tiene al lograr extensiones
del conjunto de números racionales adjuntando un numero irracional
a
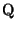 . .
Considere el conjunto
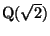 definido mediante la adjunción del número definido mediante la adjunción del número
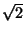 a a
Se puede probar que
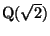 con las operaciones usuales de con las operaciones usuales de
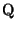 es también un campo. A su vez, es también un campo. A su vez,
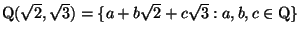 es también un subcampo del conjunto de los números reales obtenido
de la adjunción de
es también un subcampo del conjunto de los números reales obtenido
de la adjunción de  y y  que es una extensión de que es una extensión de
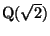 . El lector podrá comprobar fácilmente
que ambas extensiones junto con las operaciones usuales de suma y producto,
forman subcampos del conjunto de los números reales . El lector podrá comprobar fácilmente
que ambas extensiones junto con las operaciones usuales de suma y producto,
forman subcampos del conjunto de los números reales
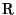 . .
El diagrama anterior representa la extensión de campos mencionada.
Una vez establecido el concepto de extensión de campos debemos
recordar la definición de numero algebraico y número trascendente.
Sea 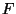 un campo y un campo y 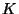 una extensión. Sea una extensión. Sea 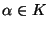 . Si existen polinomios con coeficientes en . Si existen polinomios con coeficientes en 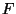 que tienen a que tienen a 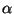 como raíz, como raíz, 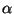 se llama algebraico sobre se llama algebraico sobre 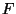 . En caso contrario . En caso contrario 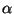 se llama trascendente sobre se llama trascendente sobre 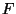 . .
Algunos ejemplos de esta definición son los siguientes:
-
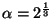 es algebraico sobre es algebraico sobre 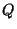 pues satisface la ecuación pues satisface la ecuación 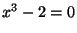 . .
- En 1873 Hermite demostró que
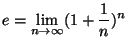 es trascendente
sobre es trascendente
sobre 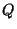 . La demostración de este resultado se puede encontrar en [4]
página 72. . La demostración de este resultado se puede encontrar en [4]
página 72.
- En 1881 Lindeman demostró que el número
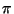 es trascendente sobre es trascendente sobre 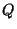 . La demostración se puede encontrar en [4] página 74. . La demostración se puede encontrar en [4] página 74.
- En 1929 Guelfand probó que
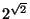 es tracendente sobre es tracendente sobre 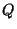 , un problema propuesto por Hilbert. En general , se probó que
si , un problema propuesto por Hilbert. En general , se probó que
si
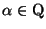 y y
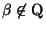 entonces entonces 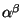 es trascendental sobre es trascendental sobre
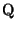 . .
Si 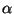 es algebraico sobre es algebraico sobre 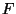 entonces existe un único polinomio entonces existe un único polinomio 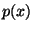 mónico (con coeficiente principal igual a 1), irreducible
sobre mónico (con coeficiente principal igual a 1), irreducible
sobre 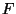 que tiene a que tiene a 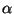 como raíz y tal que cualquier otro polinomio que tenga a como raíz y tal que cualquier otro polinomio que tenga a
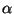 como raíz, será divisible por como raíz, será divisible por 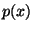 . Este polinomio se llama el polinomio minimal de . Este polinomio se llama el polinomio minimal de 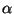 en en ![$F[\alpha]$](img33.gif) o sobre o sobre 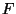 . .
Se tiene ya el lenguaje matemático necesario para enunciar un criterio
de constructibilidad. Se omite su demostración pero se remite al
lector interesado a [3] para encontrar una justificación exhaustiva.
Para que un número real 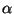 sea constructible es necesario que su polinomio mínimo sobre sea constructible es necesario que su polinomio mínimo sobre
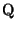 tenga grado igual a una potencia de 2. tenga grado igual a una potencia de 2.
Este resultado es increiblemente fuerte pues reduce el problema de comprobar
la constructibilidad de un numero 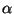 a la verificación del grado de un polinomio. Se logra así
un punto de unión entre el álgebra y la geometría. Además
sorprende el hecho de ver como una rama de la matemática tan abstarcta
como la teoría de Galois se liga con otra totalmente gráfica
e intuitiva como es la geometría. a la verificación del grado de un polinomio. Se logra así
un punto de unión entre el álgebra y la geometría. Además
sorprende el hecho de ver como una rama de la matemática tan abstarcta
como la teoría de Galois se liga con otra totalmente gráfica
e intuitiva como es la geometría.
El lector puede darse cuenta del porque otros autores han omitido referirse
a la justificación teórica de la imposibilildad de las construcciones
mencionadas. Si se toma en cuenta que se han omitido los detalles de las
demostraciones de todas las afirmaciones enunciadas, puede ver que el
tema no es sencillo de exponer.
1 2
3 4
5 6 7
8 9
|

