Operaciones con fracciones 1/3

| Luis A Acuña P  | Revista Digital Matemática, Educación e Internet |

Cuando  los denominadores son primos relativos

Como otro ejemplo, veamos la suma de las fracciones 3/4 y 2/5. Primero, las fracciones se representan así:

 

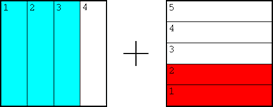
Luego las particiones de una se copian a la otra para representar el denominador común, 20:

 

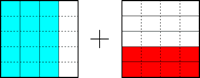
Por último, los veinteavos ``vuelan'' de la figura anterior y se posan, en orden, sobre la siguiente:

 

Vemos entonces que

$${\textstyle\frac{3}{4}}$$ + $${\textstyle\frac{2}{5}}$$ = $${\textstyle\frac{15}{20}}$$ + $${\textstyle\frac{8}{20}}$$ = $${\textstyle\frac{23}{20}}$$ = 1$${\textstyle\frac{3}{20}}$$.

En los dos ejemplos anteriores los denominadores eran primos relativos; es decir, no tenían divisores comunes. Esto es equivalente a decir que el mínimo común denominador de las fracciones es simplemente el producto de los denominadores.

En general, si en las fracciones a/b y c/d los denominadores b y d son primos relativos, entonces el mínimo común denominador será su producto, bd. Podemos representar a/b con franjas verticales y c/d con franjas horizontales (o viceversa), y al entrecruzar las particiones estaremos dividiendo el cuadrado unidad en bd piezas de igual tamaño, de las cuales ad piezas corresponderán a a/c y bc piezas corresponderán a c/d. En total serán ad + bc piezas de un total (en la unidad) de bd:

$${\frac{a}{b}}$$ + $${\frac{c}{d}}$$ = $${\frac{ad}{bd}}$$ + $${\frac{bc}{bd}}$$ = $${\frac{ad+bc}{bd}}$$.

 

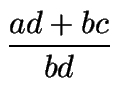Revista digital Matemática, Educación e Internet.
Derechos Reservados