
|

|
Ya tenemos listo el diseño visual más complejo: representar el denominador común de dos fracciones (en realidad el cociente de fracciones también será complicado). Gran parte de lo que dijimos en la sección anterior, sobre sumas, se aplica también a la resta de fracciones.
La principal diferencia ahora es que las piezas no vienen de ambas fracciones para reunirse todas juntas en el cuadro del resultado. Más bien las piezas de la segunda fracción (el sustraendo) vienen a caer en la primera fracción (el minuendo) sobre las piezas existentes y las ``matan'' (cancelan, anulan), de la última a la primera. Las piezas que ``sobrevivan'' representan la diferencia.
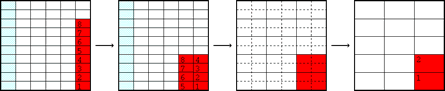
Por ejemplo, la operación de restar 1/2 - 1/3 puede visualizarse de la siguiente manera. Empezamos por las dos fracciones, con su denominador común como ya vimos:
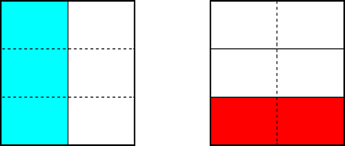
Ahora las dos piezas rojas de 1/3 (cada una representando 1/6) vienen a posarse sobre las azules de 1/2 y las anulan:
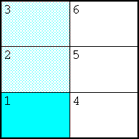
Al final queda solamente una pieza, que representa el resultado:
Si la segunda fracción es mayor que la primera, las piezas del sustraendo que sobren después de haberse anulado todo el minuendo representan el resultado, que debe interpretarse como negativo.
Para los otros casos de los denominadores (no primos entre sí) la representación de las fracciones antes de la resta es la misma que en la suma: particiones paralelas si un denominador es múltiplo del otro, o particiones perpendiculares en cualquier otro caso.
A veces será necesario simplificar el resultado. Veamos un ejemplo más: la resta de las fracciones 1/6 y 3/10. En primer lugar representamos 1/6 con particiones verticales y 3/10 con particiones horizontales, como ya es costumbre:
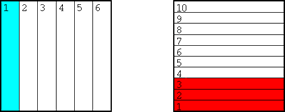
Luego representamos el denominador común entrecruzando las particiones, y vemos que 1/6 = 10/60 y 3/10 = 18/60:

Ahora las 18 piezas de la fracción derecha se posan sobre las 10 de la fracción izquierda; todas las piezas a la izquierda se cancelan, y sobran 8 piezas más (que deben considerarse negativas):
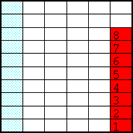
Lo anterior significa que
Ese resultado no está simplificado. Si quisiéramos reducirlo a treintavos (porque 30 es el mínimo común denominador entre 1/6 y 3/10), bastaría con hacer parejas de piezas para obtener -4/30, lo cual no es problema; de hecho ya lo hicimos en la suma de 1/4 y 1/6. Pero la mínima expresión del resultado es -2/15, que se obtiene simplifando por un factor de 4. Eso es más complicado geométricamente, porque hacer grupos de cuatro piezas no es tan directo: cada columna tiene diez piezas y cada fila tiene seis, de modo que no se pueden hacer grupos de cuatro piezas verticales ni grupos de cuatro piezas horizontales.
Deben ser grupos de dos por dos piezas, porque el factor común entre el numerador -8 y el denominador 60, es decir, 4, no es divisor de 6 ni de 10, sino que toma un factor 2 de 6 y otro factor 2 de 10. Por eso la fracción debe simplificarse eliminando la mitad de las particiones verticales y la mitad de las horizontales, luego de reubicar algunas de las piezas sobrantes:
1 2 3 4 5 6 7 8 9 10 11 12
Revista digital Matemática, Educación e Internet.
Derechos Reservados