
|

|
1 2 3 4 5 6 7 8 9 10 11 12
Los casos que ya mencionamos (que los denominadores sean primos relativos, o que uno sea múltiplo del otro), son casos extremos en cierto sentido. En efecto, si denotamos con
mcd![]() (b, d ) al máximo común divisor de los denominadores de a/b y c/d, entonces se sabe que
(b, d ) al máximo común divisor de los denominadores de a/b y c/d, entonces se sabe que
Los otros casos,
1 < mcd![]() (b, d ) < min(b, d ), se dan cuando b y d tienen algún divisor común mayor que 1, pero ni b es múltiplo de d ni viceversa. En esos casos, el mínimo común denominador de las fracciones a/b y c/d es igual al mínimo común múltiplo entre los denominadores b y d, que es
(b, d ) < min(b, d ), se dan cuando b y d tienen algún divisor común mayor que 1, pero ni b es múltiplo de d ni viceversa. En esos casos, el mínimo común denominador de las fracciones a/b y c/d es igual al mínimo común múltiplo entre los denominadores b y d, que es
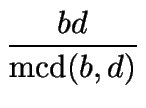 .
.
Si denotamos
m = mcd![]() (b, d ), entonces b = mp y d = mq, con p y q primos entre sí, y la ecuación anterior dice
(b, d ), entonces b = mp y d = mq, con p y q primos entre sí, y la ecuación anterior dice
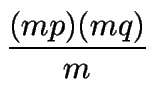 = mpq.
= mpq.
Entonces el mínimo común denominador de a/b y c/d es
MCM![]() (b, d )= mpq, que también es igual a bq y a dp. Esto significa que para sumar las fracciones usando el mínimo común denominador es necesario amplificar la primera por un factor de q y la segunda por un factor de p:
(b, d )= mpq, que también es igual a bq y a dp. Esto significa que para sumar las fracciones usando el mínimo común denominador es necesario amplificar la primera por un factor de q y la segunda por un factor de p:
Por ejemplo, las fracciones 1/4 y 1/6 están en esta situación: los denominadores no son primos relativos ni uno de ellos es múltiplo del otro. Su máximo común divisor es
m = mcd![]() (4, 6) = 2, y sus factorizaciones son
b = 4 = 2×2 y
d = 6 = 2×3, con p = 2 y q = 3 primos entre sí. El mínimo común denominador es
MCM
(4, 6) = 2, y sus factorizaciones son
b = 4 = 2×2 y
d = 6 = 2×3, con p = 2 y q = 3 primos entre sí. El mínimo común denominador es
MCM![]() (4, 6) = mpq = 2×2×3 = 12, y para sumar las fracciones debe amplificarse la primera fracción por 3 y la segunda por 2:
(4, 6) = mpq = 2×2×3 = 12, y para sumar las fracciones debe amplificarse la primera fracción por 3 y la segunda por 2:
Todo esto es rutinario. Pero si tratamos de visualizar la operación de tomar el mínimo común denominador en este ejemplo nos encontramos con una traba. Empecemos por graficar 1/4 y 1/6 individualmente:
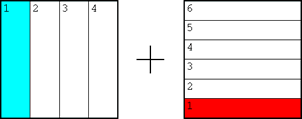
Ahora amplificamos la primera fracción por 3 y la segunda por 2:
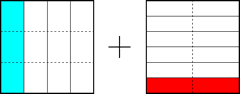
¿Y ahora? Ya tenemos 1/4 = 3/12 a la izquierda y 1/6 = 2/12 a la derecha. Es claro que la suma es 5/12, pero no podemos visualizarlo tan naturalmente como antes porque ahora los doceavos de la izquierda no tienen la misma forma que los de la derecha.
Hay dos soluciones sencillas:

Así tenemos veinticuatroavos en cada fracción, y todos del mismo tamaño. Podemos proceder como en el primer caso (denominadores primos entre sí) para obtener:
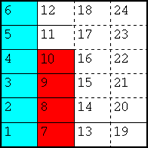
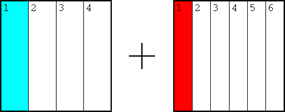
... para luego amplificar la primera fracción por 3 y la segunda por 2, siempre en la misma dirección:
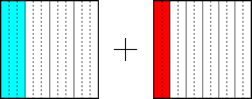
... y finalmente proceder como en el segundo caso (un denominador múltiplo del otro):
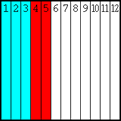
La primera solución tiene el inconveniente de que no era necesario tomar un denominador común de 24: bastaba con 12. Y la segunda tiene la desventaja de que el espacio no se aprovecha bien y las franjas resultan demasiado delgadas incluso para este denominador común tan pequeño. Con todo, la primera tal vez es preferible, reconociendo que el resultado puede simplificarse.
¿Pero cómo podría optimizarse el uso del espacio con un denominador común 12? Parece que será necesaria una representación tridimensional. En efecto, en el primer ejemplo, al representar los denominadores 2 y 3, primos relativos, se necesitaron cortes transversales para representar su producto por medio del cruce de cortes. Ahora, si en las fracciones a/b y c/d los denominadores se factorizan b = mp y d = mq como observamos, entonces son tres los factores que deben representarse perpendicularmente: m, p y q. La solución: un cubo unitario.
Por ejemplo, las fracciones 1/4 y 1/6 (m = 2, p = 2, q = 3) pueden verse así:
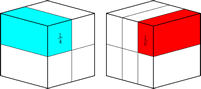
El factor común entre los denominadores, m = 2, crea una partición horizontal alrededor de cada cuadrado. El factor extra en el denominador de la primera fracción, p = 2, crea una partición vertical por la cara derecha, y el factor extra en el segundo denominador, q = 3, crea una vertical por la cara izquierda.
Copiando ahora las particiones verticales logramos representar el mínimo común denominador en una forma concisa y uniforme:
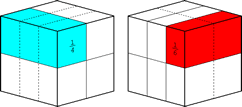
Así el cubo unitario resulta dividido en doce ``cubitos'' (claro que no son cubos sino prismas). A la izquierda tenemos 1/4 = 3/12 y a la derecha 1/6 = 2/12, con la importante característica adicional de que todos los ``cubitos'' tienen la misma forma.
Finalmente, la suma es 5/12:
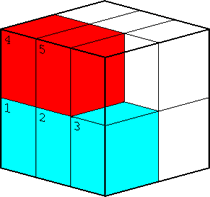
En general, dadas las fracciones a/b y c/d, donde el máximo común divisor de los denominadores es
m = mcd![]() (b, d ) y los denominadores se factorizan b = mp y d = mq, las fracciones pueden representarse como dos cubos con m franjas horizontales, p franjas verticales por la cara frontal derecha y q franjas verticales por la cara frontal izquierda:
(b, d ) y los denominadores se factorizan b = mp y d = mq, las fracciones pueden representarse como dos cubos con m franjas horizontales, p franjas verticales por la cara frontal derecha y q franjas verticales por la cara frontal izquierda:
![\begin{picture}(42,35)
\linethickness{0.4pt}
\multiput(0,5)(0,25){2}{\line(4,-1)...
...}} \put(6,2){\vector(-4,1){8}}
\put(8,1.5){\makebox(0,0)[cc]{$q$}}
\end{picture}](img35.gif)
Esta representación es probablemente la más concisa desde el punto de vista matemático. Sin embargo, tiene algunas desventajas prácticas: Por una parte, no es tan fácil programar una animación en la que los ``cubitos'' vuelan hasta posarse en orden en el cubo de resultado. Por otra parte, puede suceder que en el resultado los cubos del frente tapen a los del fondo, o los de encima a los de abajo, y no sea claro cuántos hay en total. Y aún más importante: es muy cuestionable si esta representación tendrá verdadero valor pedagógico. ¿Será claro para un pre-adolescente lo que se quiere representar con estos cubos, y será esta la mejor manera de enseñarle el proceso de tomar mínimo común denominador antes de sumar fracciones?
Para efectos de nuestro programa, optaremos por quedarnos con la primera opción que mencionamos arriba: si ningún denominador es múltiplo del otro, trabajar como si los denominadores fueran primos entre sí. Vimos en el ejemplo que el resultado era 10/24, así que la simplificación a 5/12 puede hacerse a posteriori: las diez piezas pueden agruparse en pares de modo que queden cinco de ellas, cada una representando un doceavo. Matemáticamente, el proceso será
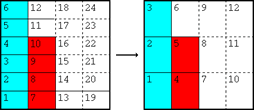
Simplificar a posteriori no es una falta tan grave; de hecho puede ser necesario aunque se trabaje con el mínimo común denominador, como en el caso de
En estos dos ejemplos, aún usando el mínimo común denominador la fracción resultante no está en su forma más simple. Simplificar después de sumar, entonces, será ocasionalmente necesario de todas maneras.
1 2 3 4 5 6 7 8 9 10 11 12
Revista digital Matemática, Educación e Internet.
Derechos Reservados