| 1
2 3 4
5 6 7
8 9 10
11 12 13 14
15 16
Resolución de la Relación de Recurrencia
Dada la sucesión:
sujeta a las condiciones iniciales 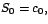
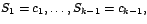 el polinomio definido por la matriz de orden el polinomio definido por la matriz de orden
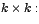
está dado por4:
Supongamos que la ecuación característica tiene 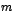 soluciones
distintas dos a dos soluciones
distintas dos a dos
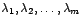 con
multiplicidades algebraicas con
multiplicidades algebraicas
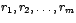 respectivamente. Bajo
estas condiciones sabemos que: respectivamente. Bajo
estas condiciones sabemos que:
con:
donde cada
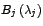 es un bloque de Jordan de orden es un bloque de Jordan de orden
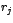 y y 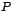 es la matriz de transformación de semejanza de la forma
canónica de Jordan de es la matriz de transformación de semejanza de la forma
canónica de Jordan de 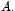 Además por el teorema 4 tenemos que: Además por el teorema 4 tenemos que:
Por otra parte, para determinar las columnas de la matriz 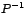 , hemos
observado en los casos particulares dos por dos y tres por tres, que por cada
valor propio , hemos
observado en los casos particulares dos por dos y tres por tres, que por cada
valor propio 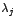 de multiplicidad algebraica de multiplicidad algebraica 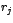 se forman se forman
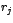 columnas de columnas de 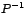 , la primera de ellas corresponde al vector propio , la primera de ellas corresponde al vector propio
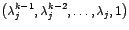 asociado a
asociado a 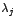 y las otras y las otras 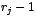 columnas están constituidas
por columnas están constituidas
por 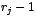 vectores propios generalísimos asociados a vectores propios generalísimos asociados a 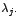
El número máximo de vectores propios generalísimos que es
necesario encontrar en este método, es igual a 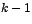 y lo anterior ocurre
cuando de la ecuación característica se obtiene una única
solución. Si a lo sumo se requieren y lo anterior ocurre
cuando de la ecuación característica se obtiene una única
solución. Si a lo sumo se requieren 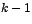 vectores propios
generalísimos, a continuación se explicará cómo es posible
encontrar estos vectores. vectores propios
generalísimos, a continuación se explicará cómo es posible
encontrar estos vectores.
En la sección  se probó, que para el caso dos por dos el vector
propio generalísimo requerido es se probó, que para el caso dos por dos el vector
propio generalísimo requerido es
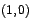 . En la
sección . En la
sección 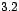 se concluyó que los vectores propios generalísimos
asociados a se concluyó que los vectores propios generalísimos
asociados a 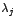 para el caso tres por tres son para el caso tres por tres son
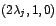 y y
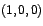 . Utilizando un método
análogo al de las secciones 3.1 y 3.2 se puede inferir que para el caso
cuatro por cuatro los vectores propios generalísimos asociados a . Utilizando un método
análogo al de las secciones 3.1 y 3.2 se puede inferir que para el caso
cuatro por cuatro los vectores propios generalísimos asociados a
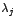 son son
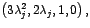
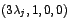 y y
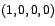 , para el
caso cinco por cinco son , para el
caso cinco por cinco son
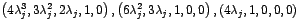 y y
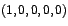 y para
el caso seis por seis corresponden a y para
el caso seis por seis corresponden a
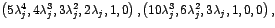
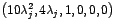 , ,
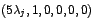 y y
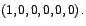
Si formamos por cada grupo de vectores añadiendo el vector propio
original, una matriz de coef icientes por f ila para
cada potencia de 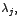 se obtiene lo siguiente: se obtiene lo siguiente:
La matriz
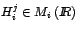
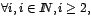 representa la matriz de coef icientes del vector
propio original y los vectores propios generalísimos asociados a representa la matriz de coef icientes del vector
propio original y los vectores propios generalísimos asociados a
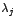 , para el caso , para el caso 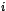 por por 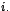
Lo interesante de cada una de estas matrices triangulares superiores, radica
en sus 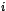 diagonales no nulas. Observe por ejemplo las diagonales no nulas
de la matriz diagonales no nulas. Observe por ejemplo las diagonales no nulas
de la matriz 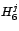 , el triángulo numérico que estas forman viene
dado por: , el triángulo numérico que estas forman viene
dado por:
que corresponde al triángulo de Pascal con 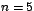 . Lo anterior
signif ica que las diagonales de la matriz . Lo anterior
signif ica que las diagonales de la matriz 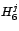 están
constituidas por coef icientes binomiales. están
constituidas por coef icientes binomiales.
En términos más generales, es posible concluir por inducción
f inita que:
La matriz 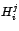 del vector propio original y los vectores
propios generalísimos asociados a del vector propio original y los vectores
propios generalísimos asociados a 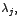 nos permite
completar las nos permite
completar las 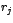 columnas de columnas de 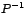 por cada por cada 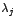 con
con
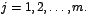 Finalmente al hallar todas las columnas de Finalmente al hallar todas las columnas de
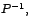 por por
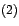 tenemos que: tenemos que:
y 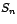 correspondería a la última fila que se obtiene
por el producto de las matrices del lado derecho en la igualdad
anterior. correspondería a la última fila que se obtiene
por el producto de las matrices del lado derecho en la igualdad
anterior.
|
![\begin{displaymath}
\mathbf{A}=\left(
\begin{array}[c]{ccccc}%
\beta_{k-1} & ...
...ots & \vdots\\
0 & 0 & \cdots & 1 & 0
\end{array}
\right)
\end{displaymath}](img223.gif)
![\begin{displaymath}
J^{n}=\left(
\begin{array}[c]{ccccc}%
\left( B_{1}\left( ...
...ight) ^{n}%
\end{array}
\right) \mbox{ por }\left( 4\right)
\end{displaymath}](img228.gif)
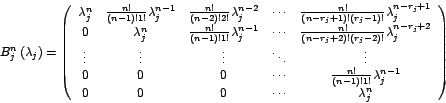
![\begin{displaymath}%
\begin{array}[c]{c}%
H_{2}^{j}=\left(
\begin{array}[c]{l...
...\\
0 & 0 & 0 & 0 & 0 & 1
\end{array}
\right)
\end{array}
\end{displaymath}](img247.gif)
![\begin{displaymath}%
\begin{array}[c]{c}%
1\\ %
\begin{array}[c]{ll}%
1 & 1
...
...]{llllll}%
1 & 5 & 10 & 10 & 5 & 1
\end{array}
\end{array}
\end{displaymath}](img253.gif)
![\begin{displaymath}
\left(
\begin{array}[c]{l}%
S_{n+k-1}\\
S_{n+k-2}\\
\...
...c_{k-2}\\
\vdots\\
c_{1}\\
c_{0}%
\end{array}
\right)
\end{displaymath}](img259.gif)
![\begin{displaymath}
H_{i}^{j}=\left(
\begin{array}[c]{llllll}
\lambda_{j}^{k...
...0 & {k-1 \choose k-1}%
\end{array}
\right) \hspace{2cm}{7}%
\end{displaymath}](img255.gif)