| 1 2
3 4 5
6 7 8 9
10
11 12 13 14
15 16
Dada la sucesión:
sujeta a las condiciones iniciales 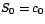 y y 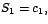 el polinomio
característico def i- el polinomio
característico def i-
nido por la matriz
![$A=\left(
\begin{array}[c]{ll}%
\beta_{1} & \beta_{0}\\
1 & 0
\end{array}
\right) $](img138.gif) corresponde a: corresponde a:
Supongamos que de la ecuación característica se obtienen dos
raíces iguales a 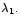 Bajo este supuesto la matriz Bajo este supuesto la matriz 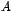 no es
diagonalizable y en consecuencia debemos encontrar la matriz de
transformación de semejanza no es
diagonalizable y en consecuencia debemos encontrar la matriz de
transformación de semejanza 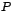 , correspondiente en la forma canónica
de Jordan, con la finalidad de calcular la potencia , correspondiente en la forma canónica
de Jordan, con la finalidad de calcular la potencia 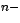 ésima
de ésima
de 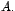
Por un resultado de la primera parte de este artículo [8] sabemos que:
por ende la primera columna de la matriz 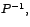 está formada por el
vector está formada por el
vector
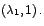 La segunda columna de La segunda columna de 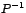 se
obtiene al hallar un vector propio generalísimo asociado a se
obtiene al hallar un vector propio generalísimo asociado a 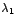 ,
para ello resolvamos el siguiente sistema de ecuaciones lineales: ,
para ello resolvamos el siguiente sistema de ecuaciones lineales:
dado que el determinante principal
![$\triangle=\left\vert
\begin{array}[c]{ll}%
\left( \beta_{1}-\lambda_{1}\right) & \beta_{0}\\
1 & -\lambda_{1}%
\end{array}
\right\vert =0$](img145.gif) por ser por ser 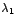 raíz del polinomio característico,
el sistema tiene inf inidad de soluciones, que quedan determinadas
al resolver cualquiera de ambas ecuaciones, al tomar la segunda de ellas se
obtiene que: raíz del polinomio característico,
el sistema tiene inf inidad de soluciones, que quedan determinadas
al resolver cualquiera de ambas ecuaciones, al tomar la segunda de ellas se
obtiene que:
Si 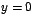 se concluye que el vector se concluye que el vector
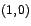 es un vector
generalísimo asociado a es un vector
generalísimo asociado a 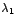 y en consecuencia: y en consecuencia:
Luego:
y f inalmente:
|
![\begin{displaymath}%
\begin{array}[c]{l}%
\left( A-\lambda_{1}I_{2}\right) \le...
...a_{1}\\
x-\lambda_{1}y=1
\end{array}
\right.
\end{array}
\end{displaymath}](img144.gif)
![\begin{displaymath}%
\begin{array}[c]{l}%
A=P^{-1}\cdot J\cdot P\mbox{ con }J=...
...-1\right) \lambda_{1}^{n}%
\end{array}
\right)
\end{array}
\end{displaymath}](img150.gif)