| 1 2 3
4 5 6
7 8 9
10
11 12 13 14
15 16
Introducción:
En la primera parte de este trabajo se desarrolló un método para
resolver relaciones de recurrencia homogéneas lineales con coef icientes constantes, utilizando valores y vectores propios bajo ciertas
condiciones particulares.
Una relación de recurrencia de este tipo es aquella de la forma:
siendo los 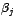 números reales f ijos números reales f ijos 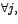
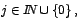
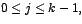 que junto con las que junto con las
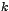 condiciones iniciales: condiciones iniciales:
determinan de manera única los elementos de una sucesión
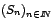 . .
Esta relación de recurrencia se puede expresar mediante un sistema de
ecuaciones lineales como sigue a continuación:
que matricialmente corresponde a:
siendo,
A partir de la ecuación
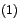 es posible
inferir2 que: es posible
inferir2 que:
de donde si se determina la potencia 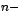 ésima de ésima de 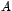 , la relación de
recurrencia queda resuelta al igualar la f ila , la relación de
recurrencia queda resuelta al igualar la f ila 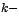 ésima de
ambas matrices ésima de
ambas matrices 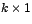 en la expresión anterior. en la expresión anterior.
En la primera parte del artículo, se abordó un método de trabajo
basado en suponer que la matriz 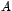 era diagonalizable, esto con la
f inalidad de poder calcular era diagonalizable, esto con la
f inalidad de poder calcular 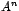
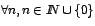 de forma directa. Efectivamente se logró demostrar
que de forma directa. Efectivamente se logró demostrar
que 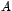 es diagonalizable sí y solo sí todos sus valores propios son
de multiplicidad algebraica igual a uno y bajo este supuesto se ideó un
algoritmo que condujo a una relación general para resolver una
relación de recurrencia homogénea lineal con coef icientes
constantes de orden es diagonalizable sí y solo sí todos sus valores propios son
de multiplicidad algebraica igual a uno y bajo este supuesto se ideó un
algoritmo que condujo a una relación general para resolver una
relación de recurrencia homogénea lineal con coef icientes
constantes de orden 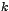 . .
Aunque los resultados que se obtuvieron fueron bastante generales, me
pareció necesario completar este trabajo, tratando el caso en el que la
matriz 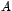 tuviera valores propios con multiplicidad algebraica mayor estricta
que uno, desde este punto de vista, concentré mis esfuerzos para dejar el
problema completamente resuelto y encontré en la teoría de matrices de
Jordan el fundamento teórico necesario con la f inalidad de
lograr dicho objetivo. tuviera valores propios con multiplicidad algebraica mayor estricta
que uno, desde este punto de vista, concentré mis esfuerzos para dejar el
problema completamente resuelto y encontré en la teoría de matrices de
Jordan el fundamento teórico necesario con la f inalidad de
lograr dicho objetivo.
|
![\begin{displaymath}
\left\{
\begin{array}[c]{l}%
S_{n+k}=\beta_{k-1}S_{n+\lef...
...ight) }\\
\vdots\\
S_{n+1}=S_{n+1}%
\end{array}
\right.
\end{displaymath}](img9.gif)
![\begin{displaymath}%
\begin{array}[c]{l}%
\mathbf{A}=\left(
\begin{array}[c]{...
...ight) \mbox{ un vector en }I\!\!R^{k}.
\end{array}
\mbox{ }
\end{displaymath}](img11.gif)