Resolución de sucesiones definidas por una Relación de Recurrencia Homogénea Lineal

La diagonalización de matrices, proporciona un recurso muy eficiente para expresar a una matriz de una forma relativamente sencilla mediante una transformación de semejanza, sin embargo, como usted ya lo ha podido comprobar, constantemente en la práctica surgen matrices no diagonalizables, en donde, se hace indispensable utilizar otros medios para determinar una semejanza que permita reducirla.

Es en este sentido, donde la teoría de matrices de Jordan³ proporciona el fundamento teórico necesario para encontrar una nueva matriz no diagonal, pero especialmente sencilla, semejante a la matriz original.

En esta sección se estudiarán las principales definiciones y teoremas de esta teoría, además de algunos resultados propios, que servirán como soporte teórico para introducir el método generalizado que deseo exponerle.

Definición 1 Sea $k\in I\!\!N$ , la matriz denotada por $N_{k}=\left( n_{ij}\right) \in M_{k}\left( I\!\!R\right)$ se define por:

$\begin{displaymath} n_{ij}=\left\{ \begin{array}[c]{c}% 1\mbox{ si }j=i+1\\ 0\mbox{ si }j\neq i+1 \end{array} \right. \end{displaymath}$

es decir:

$\begin{displaymath} N_{k}=\left( \begin{array}[c]{ccccc}% 0 & 1 & 0 & \cdots ... ...& \cdots & 1\\ 0 & 0 & 0 & \cdots & 0 \end{array} \right) \end{displaymath}$

Para un escalar dado 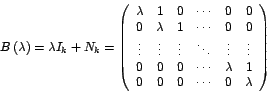$\lambda$ se def ine la matriz de bloques de Jordan denotada $B\left( \lambda\right)$ por:

$\begin{displaymath} B\left( \lambda\right) =\lambda I_{k}+N_{k}=\left( \begin{... ... 1\\ 0 & 0 & 0 & \cdots & 0 & \lambda \end{array} \right) \end{displaymath}$

de tal manera que $B\left( \lambda\right)$ es una matriz $k\times k$ con el escalar $\lambda$ en la diagonal principal, unos en la primera diagonal por encima de ella y ceros en las demás entradas.

Por ejemplo las siguientes matrices son bloques de Jordan:

$\begin{array}[c]{cccc} \overline{\lambda=2}{\left( 2\right) _{1\times1}} & ... ... & 1\\ 0 & 0 & 0 & \sqrt{2} \end{array} \right) _{4\times4}} \end{array}$

Definición 2 Una matriz de Jordan es aquella de la forma:

$\begin{displaymath} J=\left( \begin{array}[c]{ccccc}% B_{1}\left( \lambda_{1}... ...\cdots & B_{m}\left( \lambda_{m}\right) \end{array} \right) \end{displaymath}$

donde cada $B_{j}\left( \lambda_{j}\right)$ es una matriz de bloques de Jordan.

Por ejemplo las siguientes matrices son matrices de Jordan:

$\begin{array}[c]{ccc} \overline{\mbox{Formada por dos bloques}}{\left( \beg... ...0 & 0 & -3 & 0\\ 0 & 0 & 0 & 0 & 0 & 5 \end{array} \right) } \end{array}$

Teorema 1 Toda matriz cuadrada es semejante a una matriz triangular superior de la forma:

$\begin{displaymath}T=\left(\begin{array}[c]{ccccc} T_{1} & 0 & 0 & \cdots & 0\\... ...& \vdots\\ 0 & 0 & 0 & \cdots & T_{k} \end{array} \right) \end{displaymath}$

donde cada matriz $T_{j}$ $\forall j\in I\!\!N,1\leq j\leq k$ es una matriz triangular superior con elementos $\lambda_{j}$ en la diagonal principal, el orden de $T_{j}$ es la multiplicidad algebraica de $\lambda_{j}$ como valor propio de y es el número de valores propios diferentes.

Teorema 2 Toda matriz triangular superior con los elementos de su diagonal principal iguales a $\lambda$ es semejante a una matriz de Jordan de la forma:

$\begin{displaymath}\left(\begin{array}[c]{ccccc} B_{1}\left( \lambda\right) & 0... ...0 & \cdots & B_{m}\left( \lambda\right) \end{array} \right) \end{displaymath}$

Para efectos de este trabajo, los teoremas 1 y 2 se enuncian sin una demostración formal, sin embargo, si el lector está interesado le recomiendo consultar el libro $\lq\lq$ Applied Linear Algebra por B. Noble, de la editorial Prentice-Hall.

Teorema 3 (Forma Canónica de Jordan) Toda matriz cuadrada es semejante a una matriz de Jordan de la forma:

$\begin{displaymath} J=\left( \begin{array}[c]{ccccc}% B_{1}\left( \lambda_{1}... ...\cdots & B_{m}\left( \lambda_{m}\right) \end{array} \right) \end{displaymath}$

donde cada $\lambda_{j}$ $\forall j\in I\!\!N,1\leq j\leq m$ es un valor propio de

En el teorema 3 un valor propio $\lambda_{j}$ $\forall j\in I\!\!N,1\leq j\leq m$ puede aparecer en más de un bloque de Jordan, pero el número de bloques de Jordan que contienen a $\lambda_{j}$ es igual a la dimensión del subespacio propio asociado a $\lambda_{j}$ .

proof

Por el teorema 1 la matriz es semejante a una matriz triangular superior de la forma:

$\begin{displaymath}T=\left(\begin{array}[c]{ccccc} T_{1} & 0 & 0 & \cdots & 0\\... ...& \vdots\\ 0 & 0 & 0 & \cdots & T_{k} \end{array} \right) \end{displaymath}$

donde cada $T_{j}$ es una matriz triangular superior con elementos $\lambda_{j}$ en la diagonal principal, siendo $\lambda_{j}$ un valor propio de

, es decir, existe una matriz invertible

tal que:

$\begin{displaymath} T=Q\cdot A\cdot Q^{-1} \hspace{2cm}{*}% \end{displaymath}$

A su vez por el teorema 2 $T_{j}$ $\forall j\in I\!\!N,1\leq j\leq k$ es semejante a una matriz de Jordan de la forma:

$\begin{displaymath} J_{j}=\left( \begin{array}[c]{ccccc}% B_{1}\left( \lambda... ...ts & B_{m_{j}}\left( \lambda_{j}\right) \end{array} \right) \end{displaymath}$

en cuyo caso, por def inición de semejanza, existe una matriz $R_{j}$ invertible tal que:

$\begin{displaymath} J_{j}=R_{j}\cdot T_{j}\cdot R_{j}^{-1} \hspace{2cm}{**}% \end{displaymath}$

Def inamos una matriz

de la siguiente manera:

$\begin{displaymath} R=\left( \begin{array}[c]{ccccc}% R_{1} & 0 & 0 & \cdots ... ... \vdots\\ 0 & 0 & 0 & \cdots & R_{k}% \end{array} \right) \end{displaymath}$

es notable que:

$\begin{displaymath} R^{-1}=\left( \begin{array}[c]{ccccc}% R_{1}^{-1} & 0 & 0... ...ts\\ 0 & 0 & 0 & \cdots & R_{k}^{-1}% \end{array} \right) \end{displaymath}$

y en consecuencia:

$% \begin{array}[c]{l}% R\cdot\left( Q\cdot A\cdot Q^{-1}\right) \cdot R^{-1}\... ..._{k}% \end{array} \right) =J\mbox{ por }\left( \ast\ast\right) \end{array}$

La cual constituye una matriz de Jordan, donde si se considera a $P=R\cdot Q$ se tiene que:

$\begin{displaymath}% \begin{array}[c]{l}% P\cdot A\cdot P^{-1}=J\\ \Rightarrow A\sim J \end{array} \end{displaymath}$

Definición 3 A la matriz del teorema 3, se le llama forma canónica de Jordan de la matriz

El teorema 3 nos garantiza con certeza que para cualquier matriz cuadrada es posible encontrar su forma canónica de Jordan, sin embargo, ¿cuál es el procedimiento que se aplica para ello?, a continuación se utilizará un ejemplo particular para explicar la forma en como se obtiene la matriz de transformación de semejanza

example

Encuentre una matriz en la forma canónica de Jordan que sea semejante a:

$\begin{displaymath} A=\left( \begin{array}[c]{cccc}% 2 & 1 & 0 & 1\\ 1 & 3 ... ...\\ 0 & 1 & 2 & 1\\ 1 & -1 & -1 & -1 \end{array} \right) \end{displaymath}$

y determine la matriz de transformación de semejanza

Solución:

En primera instancia la ecuación característica de corresponde a:

$\begin{displaymath}% \begin{array}[c]{l}% \lambda\left( \lambda-2\right) ^{3}=0\\ \Rightarrow\lambda=2\vee\lambda=0 \end{array} \end{displaymath}$

en cuyo caso los valores propios de

son $\lambda_{1}=2$ de multiplicidad algebraica tres y $\lambda_{2}=0$ de multiplicidad algebraica uno. Los subespacios propios asociados a estos eigenvalores vienen dados por:

$\begin{displaymath} E_{\lambda_{1}}=Gen\left( \left\{ \left( 1,0,1,0\right) \r... ...}}=Gen\left( \left\{ \left( 0,1,0,-1\right) \right\} \right) \end{displaymath}$

De acuerdo a las multiplicidades algebraicas de los valores propios, se puede intuir la forma canónica de Jordan de

como la matriz:

$\begin{displaymath} J=\left( \begin{array}[c]{cccc}% \lambda_{1} & 1 & 0 & 0\... ...da_{1} & 0\\ 0 & 0 & 0 & \lambda_{2}% \end{array} \right) \end{displaymath}$

Para hallar la matriz

, supongamos que $P^{-1}=\left( X_{1},X_{2}% ,X_{3},X_{4}\right)$ con $X_{j}$ un vector columna de orden cuatro $\forall j,$

, luego por def inición de la forma canónica de Jordan tenemos que:

$\begin{displaymath}% \begin{array}[c]{l}% P\cdot A\cdot P^{-1}=J\\ \!\\ \R... ...da_{2}I_{4}\right) X_{4}=0 \end{array} \right. \end{array} \end{displaymath}$

Los sistemas de ecuaciones lineales primero y último ya fueron resueltos y una solución de dichos sistemas corresponden a los vectores propios $X_{1}=\left( 1,0,1,0\right)$ y $X_{4}=\left( 0,1,0,-1\right)$ respectivamente

El segundo sistema de ecuaciones es de la forma:

$\begin{displaymath} \left( \begin{array}[c]{cccc}% 0 & 1 & 0 & 1\\ 1 & 1 & ... ...egin{array}[c]{l}% 1\\ 0\\ 1\\ 0 \end{array} \right) \end{displaymath}$

y una solución viene dada por $X_{2}=\left( 0,\frac{3}{2},0,-\frac{1}% {2}\right)$ . F inalmente el tercer sistema de ecuaciones lineales es de la forma:

$\begin{displaymath} \left( \begin{array}[c]{cccc}% 0 & 1 & 0 & 1\\ 1 & 1 & ... ...\ \frac{3}{2}\\ 0\\ -\frac{1}{2}% \end{array} \right) \end{displaymath}$

donde $X_{3}=\left( 0,-\frac{1}{2},-\frac{1}{2},\frac{1}{2}\right)$ es una solución. En conclusión:

$\begin{displaymath} P^{-1}=\left( \begin{array}[c]{cccc}% 1 & 0 & 0 & 0\\ 0... ... 1 & -\frac{1}{2} & -1 & -\frac{3}{2}% \end{array} \right) \end{displaymath}$

En términos generales dada una matriz $A\in M_{k}\left( I\!\!R\right)$ con valores propios distintos dos a dos $\lambda_{1},\lambda_{2}% ,\ldots,\lambda_{m}$ de multiplicidad algebraica $r_{1},r_{2},\ldots,r_{m}$ respectivamente, si suponemos que los subespacios propios $E_{\lambda_{j}}$ $\forall j,j\in I\!\!N,1\leq j\leq m$ son de dimensión uno, y siendo $X_{1}^{j}$ un vector propio asociado a $\lambda_{j}$ $\forall j,j\in I\!\!N,1\leq j\leq m,$ el método expuesto en el ejemplo anterior se basa en formar y resolver los si-guientes sistemas de ecuaciones lineales:

$\begin{displaymath} \left\{ \begin{array}[c]{l}% \left( A-\lambda_{j}I_{k}\ri... ... \end{array} \right. \mbox{ con }r_{j}\neq1 \hspace{2cm}{3}% \end{displaymath}$

A cada uno de los vectores $X_{2}^{j},X_{3}^{j},\ldots,X_{r_{j}}^{j}$ se les llama vectores propios gene-ralizados o generalísimos de asociados al valor propio $\lambda_{j}.$

Hallando estos vectores propios generalísimos $\forall j,j\in I\!\!N,1\leq j\leq m$ , f inalmente la matriz $P^{-1}$ viene dada por:

$\begin{displaymath} \left( \begin{array}[c]{lllllllllllll}% X_{1}^{1} & X_{2}... ... & X_{2}^{m} & \cdots & X_{r_{m}}^{m}% \end{array} \right) \end{displaymath}$

Observe que por cada vector propio $X_{1}^{j}$ se forman $r_{j}$ columnas en $P^{-1},$ si $r_{j}=1$ entonces el único vector que se requiere para completar las $r_{j}$ columnas correspondientes en esta matriz, es el vector propio $X_{1}^{j}$ y en este caso por tanto, no se debe hallar ningún vector propio generalizado. Además, si algún subespacio propio $E_{\lambda_{j}}$ es de dimensión $t_{j}\in I\!\!N,$ $t_{j}\neq1$ existen $t_{j}$ vectores propios asociados a $\lambda_{j}$ linealmente independientes y en consecuencia se requerirían $r_{j}-t_{j}$ vectores propios generalizados, para formar las $r_{j}$ columnas correspondientes en $P^{-1}$ .

Centremos ahora nuestra atención, en cómo hallar la potencia ésima de una matriz de Jordan. Dada una matriz de Jordan de la forma:

$\begin{displaymath} J=\left( \begin{array}[c]{ccccc}% B_{1}\left( \lambda_{1}... ...\cdots & B_{m}\left( \lambda_{m}\right) \end{array} \right) \end{displaymath}$

es notable su estructura diagonal, en consecuencia por un resultado demostrado en la primera parte de este artículo, se puede inferir que:

$\begin{displaymath} J^{n}=\left( \begin{array}[c]{ccccc}% \left( B_{1}\left( ... ... \end{array} \right) \forall n,n\in I\!\!N \hspace{2cm}{4}% \end{displaymath}$

es decir, la potencia

ésima de una matriz de Jordan se puede calcular al obtener las potencias

ésimas de los bloques que la constituyen, sin embargo, ¿cómo se calculan dichas potencias?, para dar respuesta a esta pregunta se enuncia el siguiente teorema.

Teorema 4 (Potencia

ésima de un bloque de Jordan) Sea $B=\left( b_{ij}\right) \in M_{r}\left( I\!\!R\right)$ un bloque de Jordan de la forma:

$\begin{displaymath} b_{ij}=\left\{ \begin{array}[c]{l}% \lambda\mbox{ si }i=j... ...x{ si }j=i+1\\ 0\mbox{ en otro caso}% \end{array} \right. \end{displaymath}$

es decir:

$\begin{displaymath} B=\left( \begin{array}[c]{cccccc}% \lambda & 1 & 0 & \cdo... ... 1\\ 0 & 0 & 0 & \cdots & 0 & \lambda \end{array} \right) \end{displaymath}$

entonces $B^{n}=\left( c_{ij}\right) \in M_{r}\left( I\!\!R\right)$ $\forall n,n\in I\!\!N$ es tal que:

$\begin{displaymath} c_{ij}=\left\{ \begin{array}[c]{l}% \lambda^{n}\mbox{ si ... ... }l=1,2,\ldots,r-1\\ 0\mbox{ si }i>j \end{array} \right. \end{displaymath}$

es decir:

$\begin{displaymath} B^{n}=\left( \begin{array}[c]{ccccc}% \lambda^{n} & \frac... ...}\\ 0 & 0 & 0 & \cdots & \lambda^{n}% \end{array} \right) \end{displaymath}$

Prueba:
Procedamos por el primer principio de inducción.

Para $B=\left( \lambda\right) \Rightarrow B^{n}=\left( \lambda ^{n}\right)$ con lo cual queda probado el teorema en este caso.

Supongamos por hipótesis de inducción que para algún $k,k\in I\!\!N,$ $B^{k}=\left( c_{ij}^{\prime}\right)$ es tal que:

$\begin{displaymath} c_{ij}^{\prime}=\left\{ \begin{array}[c]{l}% \lambda^{k}\... ... }l=1,2,\ldots,r-1\\ 0\mbox{ si }i>j \end{array} \right. \end{displaymath}$

Probemos el teorema para . Sea $B^{k+1}=\left( c_{ij}\right) \in M_{r}\left( I\!\!R\right) :$

$B^{k+1}=B^{k}\cdot B$ por def inición de potencia de matrices

$\Rightarrow c_{ij}=\sum\limits_{h=1}^{r}c_{ih}^{\prime}b_{hj}$ por def inición del producto de matrices

Consideremos los siguientes casos:

$c_{ii}=\sum\limits_{h=1}^{r}c_{ih}^{\prime}b_{hi}=c_{i1}^{\prime}% b_{1i}+c_{i... ...+c_{ii}^{\prime }b_{ii}+c_{ii+1}^{\prime}b_{i+1i}+\ldots+c_{ir}^{\prime}b_{ri}$

$=0+0+\ldots+0+\lambda\cdot\lambda^{k}+0+\ldots+0$ $=\lambda^{k+1}$ por def inición de y la hipótesis inductiva

con $l=1,2,\ldots,r-1$

$c_{ii+l}=\sum\limits_{h=1}^{r}c_{ih}^{\prime}b_{hi+l}=c_{i1}^{\prime}% b_{1i+l... ...ime}b_{i+li+l}+c_{ii+l+1}^{\prime}b_{i+l+1i+l}+\ldots +c_{ir}^{\prime}b_{ri+l}$

$=0+0+\ldots+\frac{k!}{\left( k+1-l\right) !\left( l-1\right) !}% \lambda^{k+1-l}\cdot1+\lambda\cdot\frac{k!}{\left( k-l\right) !l!}% \lambda^{k-l}+0+\ldots+0$ por def inición de y la hipótesis inductiva

$=\frac{k!}{\left( k+1-l\right) !\left( l-1\right) !}\lambda ^{k+1-l}\left[ 1+\frac{k+1-l}{l}\right]$ $=\frac{k!}{\left( k+1-l\right) !\left( l-1\right) !}\lambda^{k+1-l}\left[ \frac{l+k+1-l}{l}\right]$

$=\frac{k!}{\left( k+1-l\right) !\left( l-1\right) !}\lambda ^{k+1-l}\left[ \fr... ...{l}\right] =\frac{\left( k+1\right) !}{\left( k+1-l\right) !l!}\lambda^{k+1-l}$

$c_{ij}=\sum\limits_{h=1}^{r}c_{ih}^{\prime}b_{hj}=c_{i1}^{\prime}% b_{1j}+c_{i... ...+c_{ij}^{\prime }b_{jj}+c_{ij+1}^{\prime}b_{j+1j}+\ldots+c_{ir}^{\prime}b_{rj}$

$=0+0+\ldots+0\cdot1+0\cdot\lambda+0+\ldots+0$ por def inición de y la hipótesis inductiva

$% latex2html id marker 3911 $\therefore c_{ij}=\left\{ \begin{array}[c]{l}% \... ...i }j=i+l\mbox{ con }l=1,2,\ldots,r-1\\ 0\mbox{ si }i>j \end{array} \right. $$

Todos los resultados expuestos con anterioridad, nos permiten crear un modelo general, a partir del cual es posible resolver relaciones de recurrencia homogéneas lineales de cualquier orden, cuando los valores propios tienen multiplicidad algebraica mayor estricta que uno. En la siguiente sección se abordará este problema para relaciones de recurrencia de orden dos y tres y f inalmente se expone el método generalizado para relaciones de orden