| 1 2
3 4 5
6 7 8 9
10
11 12 13 14
15 16
Ejemplos de Aplicación
Ejemplo 1
Definamos la sucesión recursiva
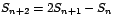 sujeta a las condiciones iniciales sujeta a las condiciones iniciales
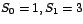 , formando el sistema de ecuaciones: , formando el sistema de ecuaciones:
se tiene que la matriz asociada al sistema es
![$A=\left(
\begin{array}[c]{cc}%
2 & -1\\
1 & 0
\end{array}
\right) $](img156.gif) y las condiciones iniciales están dadas por y las condiciones iniciales están dadas por
![$X_{0}=\left(
\begin{array}[c]{l}%
3\\
1
\end{array}
\right) .$](img157.gif) El polinomio característico de la matriz El polinomio característico de la matriz 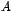 es: es:
cuya única raíz es
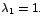 Por Por
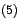 tenemos
que tenemos
que 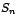 corresponde a: corresponde a:
Ejemplo 2
Def inamos la sucesión recursiva
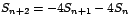 sujeta a las condiciones iniciales sujeta a las condiciones iniciales
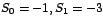 , formando el sistema de ecuaciones: , formando el sistema de ecuaciones:
se tiene que la matriz asociada al sistema es
![$A=\left(
\begin{array}[c]{cc}%
-4 & -4\\
1 & 0
\end{array}
\right) $](img166.gif) y las condiciones iniciales están dadas por y las condiciones iniciales están dadas por
![$X_{0}=\left(
\begin{array}[c]{l}%
-3\\
-1
\end{array}
\right) .$](img167.gif) El polinomio característico de la matriz El polinomio característico de la matriz 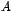 es: es:
cuya única raíz es
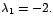 Por Por
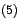 tenemos que
tenemos que 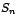 corresponde a: corresponde a:
|