El teorema de Napoleón

 

Mario Dalcín
   
 Inicio  1  2  3  4  5  6  7  8  9  10  11  12 13 14

 

 

Quinta demostración

Usaremos ahora la geometría analítica para hacer una nueva demostración del teorema de Napoleón.

Empecemos recordando la relación que vincula a la tangente del ángulo que forma dos rectas con sus respectivos coeficientes angulares.

Si las rectas $\,r\,$ y $\,r'\,$ tienen coeficientes angulares $\,m\,$ y $\,m'\,$, siendo $m=tang \alpha$, $m'=tang \beta$ y $\,\alpha\,$ y $\,\beta\,$ las medidas de los ángulos que forman las rectas $\,r\,$ y $\,r'\,$ con el eje $\,x\,$, el ángulo $\,(\vartheta)\,$ entre las dos rectas $\,r\,$ y $\,r'\,$ está dado por la relación:



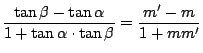$\tan \theta = \tan (\beta - \alpha)$ $=$ $\displaystyle {\frac{\tan \beta-\tan \alpha}{1+\tan \alpha \cdot \tan \beta} = \frac{m'-m}{1+mm'}}$





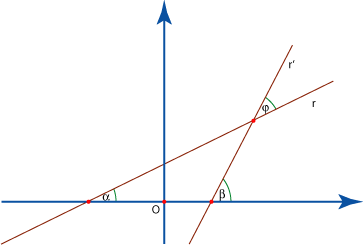
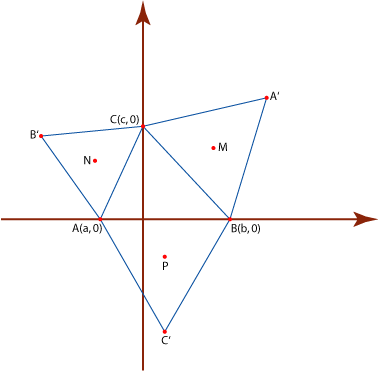
Sin pérdida de generalidad podemos asignarle a los vértices el triángulo $\,\triangle ABC\,$ las coordenadas

$\,A(a,0),B(b,0)\,$ y $\,C(0,c)\,$.

Si llamamos $\,m'\,$ al coeficiente angular de la recta $\,\overline{BC}\,$, se cumple que $\,\displaystyle {m'=\frac{-c}{b}}\,$.

El ángulo que forman las rectas $\,\overline{BA'}\,$ y $\,\overline{BC}\,$ es $\,60º\,$ y $\tan 60º=\sqrt{3}$.

Aplicando la relación previamente expuesta, si llamamos $\,m\,$ al coeficiente angular de la recta $\,\overline{BA'}\,$, podemos hallar $\,m\,$ a partir de la ecuación:

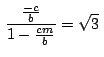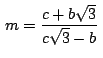$\,\displaystyle {\frac{\frac{-c}{b}}{1-\frac{cm}{b}}}=\sqrt{3}\,$, obteniendo así que $\,\displaystyle {m=\frac{c+b\sqrt{3}}{c\sqrt{3}-b}}\,$.

La ecuación de la recta $\,\overline{BA'}\,$ es entonces:

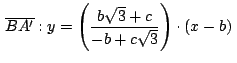
$\,\displaystyle {\overline{BA'}: y = \left(\frac{b\sqrt{3}+c}{-b+c\sqrt{3}}\right)\cdot (x-b)}\,$

Procediendo de forma análoga podemos hallar la ecuación de la recta $\,\overline{CA'}\,$:

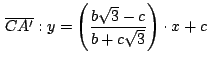
$\,\displaystyle {\overline{CA'}: y = \left(\frac{b\sqrt{3}-c}{b+c\sqrt{3}}\right)\cdot x+c}\,$

Resolviendo el sistema formado formado por las ecuaciones de las rectas $\,\overline{BA'}\,$ y $\,\overline{CA'}\,$ obtenemos las coordenadas del punto $\,A'\,$

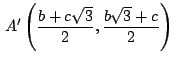$\,\displaystyle {A'\left(\frac{b+c\sqrt{3}}{2},\frac{b\sqrt{3}+c}{2}\right)}\,$,

Repitiendo el procedimiento seguido para determinar el punto $\,A'\,$ podemos hallar las coordenadas del punto $\,B'\,$ intersecando las rectas

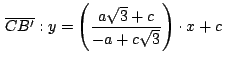
$\,\displaystyle {\overline{CB'}: y = \left(\frac{a\sqrt{3}+c}{-a+c\sqrt{3}}\right)\cdot x+c}\,$

y

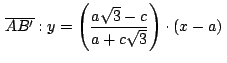
$\,\displaystyle {\overline{AB'}: y = \left(\frac{a\sqrt{3}-c}{a+c\sqrt{3}}\right)\cdot(x-a)}\,$



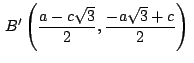obteniendo $\,\displaystyle {B'\left(\frac{a-c\sqrt{3}}{2},\frac{-a\sqrt{3}+c}{2}\right)}\,$.

Intersecando las rectas

$\,\overline{AC'}:y=-\sqrt{3}(x-a)\,$

y

$\,\overline{BC'}:y=\sqrt{3}(x-b)\,$

obtenemos las coordenadas de $\,C'\,$

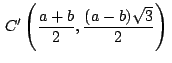$\,\displaystyle {C'\left(\frac{a+b}{2},\frac{(a-b)\sqrt{3}}{2}\right)}\,$.



Recordando ahora que si los vertices de un triángulo $\,\triangle ABC\,$ tiene coordenadas
$\,\displaystyle {A(x_{A},y_{A}),B(x_{B},y_{B}),C(x_{C},y_{C})}\,$, el baricentro de dicho triángulo tiene coordenadas:


\begin{displaymath}\displaystyle {\left(\frac{x_{A}+x_{B}+x_{C}}{3},\frac{y_{A}+y_{B}+y_{C}}{3}\right)}\end{displaymath}

podemos hallar las coordenadas de:

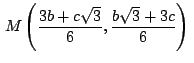$\,\displaystyle {M\left(\frac{3b+c\sqrt{3}}{6},\frac{b\sqrt{3}+3c}{6}\right)}\,$,



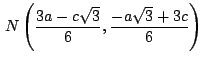$\,\displaystyle {N\left(\frac{3a-c\sqrt{3}}{6},\frac{-a\sqrt{3}+3c}{6}\right)}\,$,



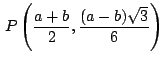$\,\displaystyle {P\left(\frac{a+b}{2},\frac{(a-b)\sqrt{3}}{6}\right)}\,$,

Por último calcular las distancias

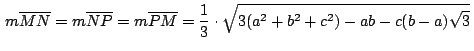$\,\displaystyle {m\overline{MN}=m\overline{NP}=m\overline{PM}=\frac{1}{3}\cdot\sqrt{3(a^{2}+b^{2}+c^{2})-ab-c(b-a)\sqrt{3}}}\,$.

 
 Inicio  1  2  3  4  5  6  7  8  9  10  11  12 13 14

 

Cidse - Revista virtual Matemática, Educación e Internet - ITCR
Derechos Reservados