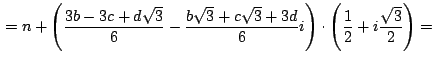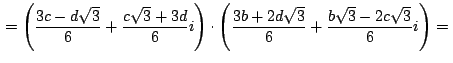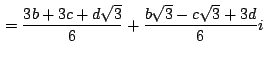|
Recurriendo a los números complejos para hacer una nueva demostración del teorema de Napoleón.
"Asociaremos al numero complejo 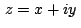 , en que , en que 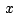 y y
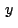 son reales e son reales e 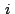 es la unidad imaginaria, el punto es la unidad imaginaria, el punto
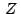 con coordenadas rectangulares con coordenadas rectangulares 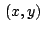 en un plano
cartesiano. El punto en un plano
cartesiano. El punto 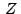 se denominara imagen, o punto
representativo, del numero complejo se denominara imagen, o punto
representativo, del numero complejo 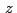 y dicho numero
recibirá el nombre de afijo, o coordenada compleja, del punto y dicho numero
recibirá el nombre de afijo, o coordenada compleja, del punto 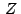 ."(Eves, 1985, pag.167) ."(Eves, 1985, pag.167)
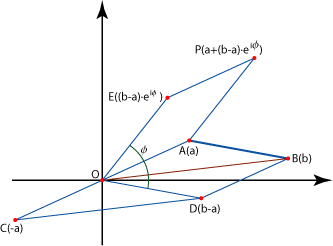
Necesitaremos también el siguiente teorema: "Si 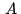 y y
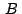 son puntos con afijos son puntos con afijos 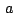 y y 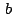 , respectivamente,
entonces , respectivamente,
entonces
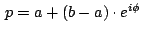 es el afijo del punto es el afijo del punto
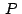 obtenido girando un ángulo obtenido girando un ángulo 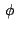 el punto el punto 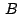 alrededor del punto
alrededor del punto  ."
(Eves, 1985, pág 174) ."
(Eves, 1985, pág 174)
Viendo el diagrama que sigue se podrá entender el por qué de la
condición.
Para el caso en que 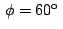 el teorema anterior nos da una
condición necesaria y suficiente para que un triángulo el teorema anterior nos da una
condición necesaria y suficiente para que un triángulo
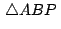 sea equilátero, y dicha condición es que los
afijos sea equilátero, y dicha condición es que los
afijos 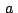 , , 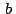 y y 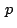 de sus vértices (sus coordenadas
complejas)
verifiquen la condición de sus vértices (sus coordenadas
complejas)
verifiquen la condición
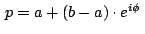 . .
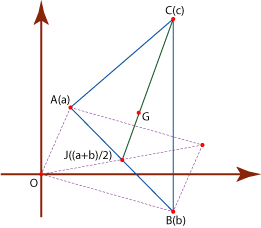
Asignándole un número complejo a cada vértice del triángulo  podemos considerar sin perdida de generalidad:
podemos considerar sin perdida de generalidad:
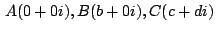
Si 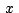 , , 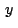 , , 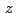 son los afijos de son los afijos de 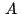 , , 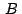 y y
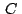 respectivamente respectivamente
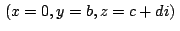 , los afijos , los afijos
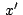 , ,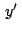 , ,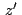 de los puntos de los puntos 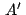 , , 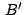 , , 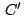 serán:
serán:
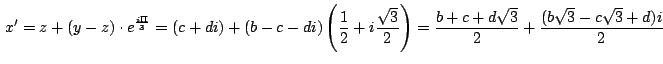
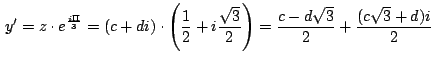
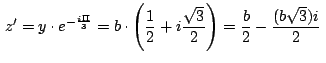 . .
Llegados aquí necesitamos de otro teorema: ``El centroide
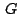 del triángulo del triángulo
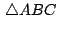 tiene como afijo tiene como afijo
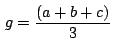 ." (Eves, 1985, pág 176) ." (Eves, 1985, pág 176)
Si 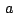 , , 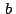 , , 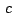 son los afijos de son los afijos de 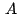 , , 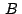 y y
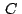 , el punto , el punto 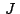 medio de medio de
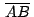 tiene como
afijo tiene como
afijo
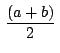 . Como el baricentro . Como el baricentro 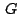 verifica que
verifica que
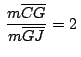 , se
cumple la siguiente relación entre los afijos de , se
cumple la siguiente relación entre los afijos de 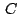 , , 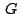 y y
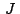 : :
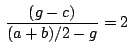
Despejando concluimos que
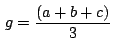 . .
Usando la condición anterior podemos hayan los afijos 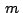 , ,
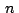 , , 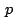 de los puntos de los puntos 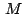 , , 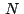 , , 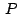 baricentros de
los triángulos baricentros de
los triángulos
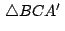 , ,
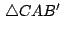 y y
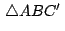 respectivamente. respectivamente.
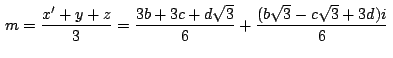 (1) (1)
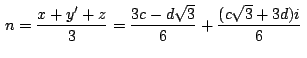
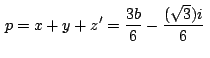
Si hallamos ahora, usando la condición necesaria y suficiente para
que un triángulo sea equilátero mencionada antes, el afijo
(coordenada compleja) del tercer vértice del triángulo equilátero
de vértices 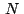 y y 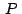 tenemos: tenemos:
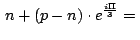
![$\,\displaystyle {=n+\left[\frac{3b}{6}-i\frac{b\sqrt{3}}{6}-\left(\frac{3c-d\sq...
...3}+3d}{6}i\right)\right]
\cdot \left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)=}\,$](img449.gif)
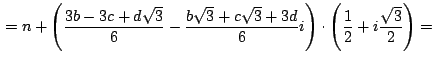
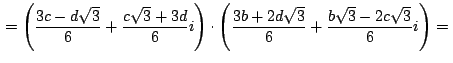
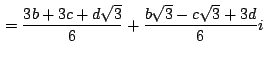
que es el afijo del punto 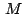 hallado antes en (1). hallado antes en (1).
Podemos concluir entonces que
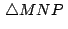 es equilátero. es equilátero.
(Demostración sugerida en de Guzmán, 1995,p.341)
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|


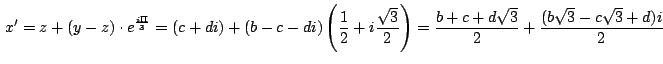
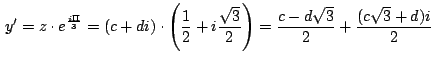
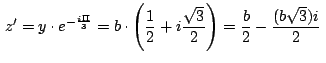 .
.
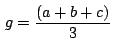 ." (Eves, 1985, pág 176)
." (Eves, 1985, pág 176)
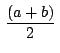 . Como el baricentro
. Como el baricentro 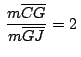 , se
cumple la siguiente relación entre los afijos de
, se
cumple la siguiente relación entre los afijos de 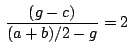
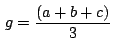 .
.

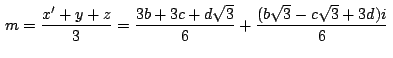 (1)
(1)
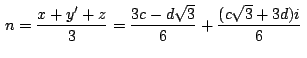
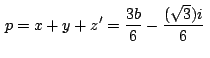
![$\,\displaystyle {=n+\left[\frac{3b}{6}-i\frac{b\sqrt{3}}{6}-\left(\frac{3c-d\sq...
...3}+3d}{6}i\right)\right]
\cdot \left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)=}\,$](img449.gif)