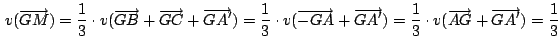|
Las rectas
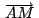 , ,
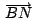 , ,
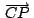 son concurrentes.
son concurrentes.
Para demostrar esta propiedad necesitaremos del teorema de Ceva:
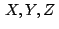 son puntos sobre los lados son puntos sobre los lados
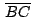 , ,
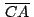 , ,
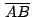 de un
triángulo de un
triángulo
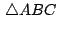 . .
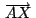 , ,
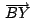 , ,
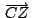 son
concurrentes son
concurrentes
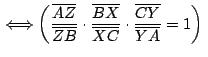
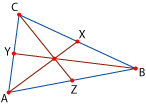
También usaremos, según vimos previamente, que el área
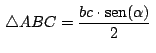
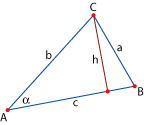
En nuestra figura:
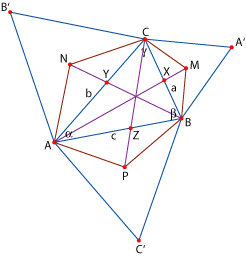
si calculamos
por el teorema de Ceva:
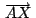 , ,
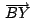 , ,
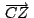 concurren, y concurren, y
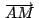 , ,
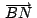 , ,
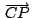 concurren concurren
 Bajo la notación dada en el Teorema de Napoleón, el Bajo la notación dada en el Teorema de Napoleón, el
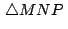 y el y el
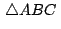 tienen el
mismo
baricentro. tienen el
mismo
baricentro.
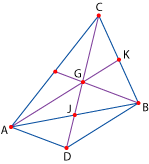
Siendo 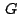 el baricentro del triángulo el baricentro del triángulo
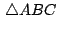 se cumplen las siguientes relaciones entre vectores:
se cumplen las siguientes relaciones entre vectores:
| i.) |
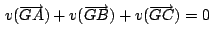
|
Sea
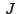 el punto medio de las diagonales el punto medio de las diagonales
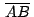 y y
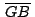 del paralelogramo del paralelogramo
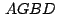
Se cumple:
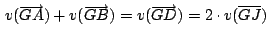
Por ser
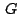 baricentro también se cumple: baricentro también se cumple:
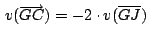
De lo anterior:
| ii.) |
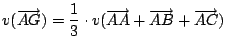
|
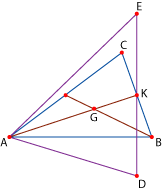
iii.)
Siendo 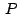 un punto cualquiera: un punto cualquiera:
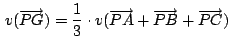
Si
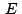 cumple que cumple que
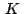 (el punto medio de (el punto medio de
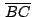 )
es punto medio de )
es punto medio de
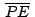 , se cumple que , se cumple que
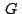 también
es baricentro de también
es baricentro de
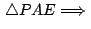 aplicando aplicando
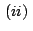 al triángulo al triángulo
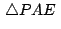 tenemos: tenemos:
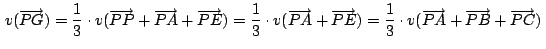
En nuestra construcción
de la misma forma
 es circuncentro de es circuncentro de
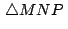 equilátero, por
lo
que equilátero, por
lo
que 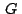 también es su baricentro también es su baricentro
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
Derechos Reservados
|
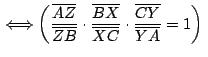

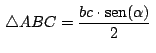


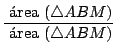
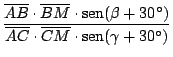
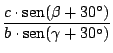
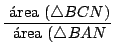
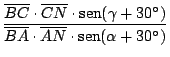
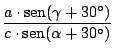
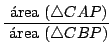
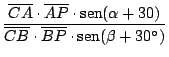
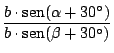
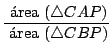
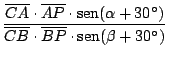
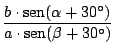
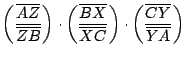
![$\displaystyle {\frac{[b \cdot \mathop{\rm sen}\nolimits (\alpha + 30^\circ)] \c...
...ma + 30^\circ)] \cdot [c
\cdot \mathop{\rm sen}\nolimits (\alpha + 30^\circ)]}}$](img161.gif)