|
Dado
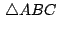 un triangulo cualquiera. Se
construyen exteriormente los triángulos equiláteros un triangulo cualquiera. Se
construyen exteriormente los triángulos equiláteros
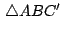 , ,
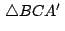 y y
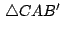 . Bajo estas
condiciones se cumple que: . Bajo estas
condiciones se cumple que:
 Los segmentos Los segmentos
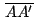 , ,
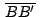 , ,
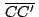 son congruentes. son congruentes.
Se deduce que los triángulos
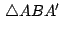 y y
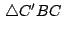 son congruentes por tener son congruentes por tener
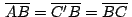 y y
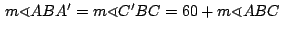 , de donde , de donde
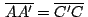 . .
De forma análoga son congruentes
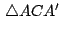 y y
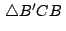 por lo que por lo que
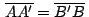 . .
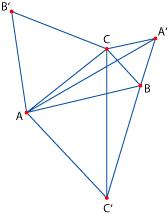
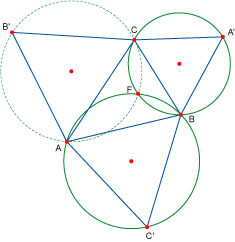
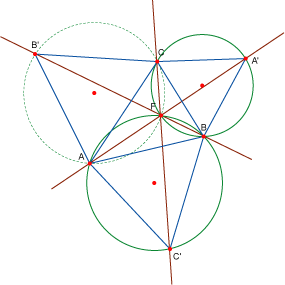
 Los círculos circunscritos a los triángulos Los círculos circunscritos a los triángulos
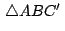 , ,
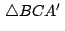 , ,
 pasan por un
mismo punto. pasan por un
mismo punto.
Si
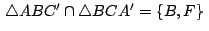 ,
como ,
como
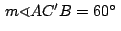 se tiene se tiene
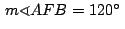 y como y como
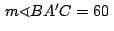 se tiene: se tiene:
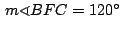 por lo
que por lo
que
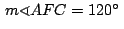 y como y como
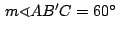 se deduce que el cuadrilátero se deduce que el cuadrilátero
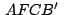 es inscriptible de donde es inscriptible de donde
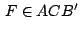 . .
Para completar la demostración debemos considerar el caso en que
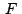 es exterior a es exterior a
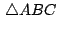 y también el caso en
que y también el caso en
que 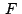 coincide con coincide con 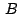 . .
 Las rectas Las rectas
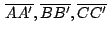 son
congruentes en son
congruentes en 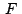 y forman y forman 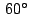 entre ellas. entre ellas.
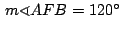 y y
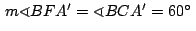 por ser ángulos inscritos que
abarcan la misma cuerda por ser ángulos inscritos que
abarcan la misma cuerda
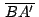 de donde: de donde:
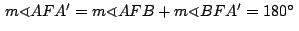 por lo que por lo que 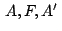 están
alineados. están
alineados.
De forma análoga 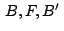 y y 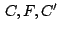 están alineados. están alineados.
La demostración quedará completa considerando el caso en que
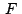 es exterior a es exterior a
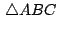 y también el caso en
que y también el caso en
que 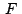 coincide con coincide con 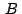 . .
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|


