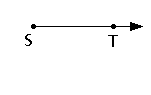En el siguiente apartado se estudiará los conceptos de segmento, semirrecta, rayo y ángulo, además de la notación que se utiliza en geometría plana para dichos conceptos. 

Por último, se especificarán cinco postulados muy importentes dentro del estudio de la geometría plana.

Actividad Interactiva

Importante:  si durante la acvtidad tiene problemas para visualizar la recta, segmento, rayo, semirrecta o ángulo; dé clic sobre el botón "Reiniciar".

1.  Dé clic sobre el botón "Segmento" y descubra qué característica(s) tiene(n) el segmento con relación a la recta?  Sugerencia:  mueva los puntos F y G del segmento.  Anote sus conclusiones.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

2.  ¿El segmento es finito o infinito?

3.  Defina con sus propias palabras segmento.

4.  Dé clic sobre el botón "Rayo" y descubra qué característica(s) tiene(n) el rayo con relación a la recta?  Sugerencia:  mueva los puntos F y G del rayo.  Anote sus conclusiones.

5.  ¿Qué indica la flecha?  ¿Podría la flecha estar señalando cualquier parte?

6.  Defina con sus propias palabras rayo.

7.  Dé clic sobre el botón "Semirrecta" y descubra qué característica(s) tiene(n) la semirrecta con relación a la recta?  Sugerencia:  mueva el punto G de la semirrecta.  Anote sus conclusiones.

8.  ¿Qué indica la flecha?  ¿Podría la flecha estar señalando cualquier parte?

9.  Defina con sus propias palabras semirrecta.

10.  Si es observador(a), se dará cuenta que el rayo y la semirrecta son muy parecidos pero: ¿cuál es la diferencia entre ellos?

11.  Dé clic sobre el botón "Ángulo" y descubra qué característica(s) tiene(n) el ángulo? Sugerencia:  mueva los puntos F y G del ángulo.  Anote sus conclusiones.

12.  ¿Existirá algún parecido entre los ángulos y las agujas de un reloj?  Mueva nuevamente los puntos F y G del ángulo para comprobarlo.

13.  ¿Qué relación tienen los ángulos con los rayos? ¿Será acaso que los ángulos están formados por rayos?  Si su respuesta es afirmativa,  ¿cuántos rayos observa en el ángulo?

14.  Defina con sus propias palabras ángulo.

En general, se dice que:

• Los segmentos son una parte de la recta, la cual se señala entre dos puntos llamados extremos del segmento.  Los segmentos son finitos y pueden ser tan grandes como se quiera.

Su representación es la siguiente:

 y se denota así:  AB.  

• Los rayos son aquella parte de la línea recta que queda a algún lado de un punto llamado origen, señalado sobre ella.

Su representación es la siguiente:

 y se denota así: .  La primera letra siempre representa el origen.

• Las semirrectas son rayos que no contienen a su origen.

Su representación es la siguiente:

 y se denota así: .  La primera letra siempre representa el origen.

Note que tanto en los rayos como en las semirrectas, el punto que no es origen, se utiliza nada más para efectos de notación, es decir, para poder darle nombre ya sea al rayo o a la semirrecta.  Dicho punto puede ubicarse en cualquier parte del rayo o  de la semirrecta. 

• Los ángulos son la unión de dos rayos.  Note que ambos rayos tienen un mismo origen, al cual se le conoce con el nombre de vértice del ángulo y a los rayos se les conoce como lados del ángulo.  Es importante señalar que siempre que se unen dos rayos, forman dos ángulos, uno de abertura más pequeña que el otro.  Observe el dibujo:

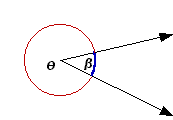
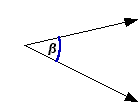
Observe que la abertura q es más grande que la abertura b.

Existen tres formas de denotar a un ángulo:

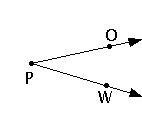
Mediante tres puntos

Ángulo OPW o Ángulo WPO. El vértice siempre va al centro. Simbólicamente se escribe: < OPW o < WPO.
Esta notación tiene un problema, pues no especifica a cual ángulo se está haciendo referencia, si al de abertura pequeña o al de abertura grande.  Para evitar este problema se sobrentiende que se hace referencia al ángulo de abertura más pequeña.   Mediante una letra del alfabeto griego
Ángulo b. Simbólicamente se escribe: < b.
Sólo con el vértice
Ángulo P. Simbólicamente se escribe: < P.
Esta notación tiene un problema, pues no especifica a cual ángulo se está haciendo referencia, si al de abertura pequeña o al de abertura grande.  Para evitar este problema se sobrentiende que se hace referencia al ángulo de abertura más pequeña.

Postulados

Un postulado es una verdad que no necesita ser demostrado.

1.  Por un punto pasan infinitas rectas.

2.  Por dos puntos diferentes pasa únicamente una recta.

3.  La intersección de dos rectas es un punto.

4.  La distancia más corta entre dos puntos diferentes es el segmento de recta que los une.

5.  Dada una recta "m" y un punto "R" fuera de la recta (ambos sobre un plano), se dice que existe una sola recta que pasa por "R" y que no interseca a "m".