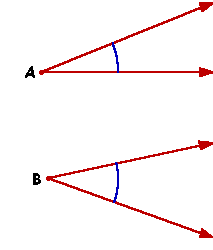
Dos ángulos cualesquiera, A y B por ejemplo, pueden ser comparados de acuerdo a sus medidas; claramente existen únicamente tres posibles resultados al compararlos: puede que el ángulo A sea mayor que el ángulo B, o bien, que el ángulo A sea menor que el ángulo B, y por último, puede suceder que ambos ángulos sean de igual medida, en cuyo caso se dice que los ángulos son congruentes.

En general, para comparar dos ángulos se debe comparar sus aberturas; el ángulo con mayor abertura será mayor que el otro, en forma similar, el ángulo con menor abertura será menor que el otro, y por último, si las aberturas de los ángulos es igual, los ángulos son congruentes.

Actividad Interactiva

Dé clic sobre el botón "Iniciar" del campo de trabajo y siga los siguientes pasos.

1.  Considere el ángulo A.

2.  Con radio arbitrario construya un círculo con centro en A.

3.  Determine el punto de intersección de cada lado del ángulo con el círculo y trace el segmento que une estos puntos.

4.  Determine la medida del segmento anteriormente construido y observe la medida del ángulo A.

5.  Considere el ángulo B, C o D dando clic sobre el botón respectivo y con el mismo radio del paso 2, realice los pasos 2, 3 y 4 para los ángulos B, C y D respectivamente.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

Mueva el punto rojo y determine la relación existente entre cada uno de los ángulos B, C y D con el ángulo A.