Para graficar flechas 3D, vamos a usar una pequeña modificación del
paquete Arrow3D de Harry Calkins
Vamos a crear una sencilla función Flecha3D[] la cual pondremos en
una celda que luego vamos a ejecutar.
Esta función dibuja un cono al final de un segmento que va de
pt1 a pt2, el tamaño del cono es un porcentaje de la
longitud del segmento. Como el cono se construye con
triángulos, se debe indicar el número de triángulos 'nlds'
El código de la función Flecha3D[] es
Flecha3D[pt1_, pt2_, nlds_, porc_, color_] := (
{aa, bb, cc} =pt2-pt1;
(*construcción de una base ortonormal pata la cabeza de la flecha*)
nrm1 = {0, 1, 0};
nrm2 = {1, 0, 0};
Which[
aa == 0 && bb == 0, nrm1 = {0, 1, 0}; nrm2 = {1, 0, 0},
aa == 0 && cc == 0, nrm1 = {1, 0, 0}; nrm2 = {0, 0, 1},
bb == 0 && cc == 0, nrm1 = {0, 0, 1}; nrm2 = {0, 1, 0},
aa == 0,
nrm1 = {1, 0, 0};
nrm2 = Cross[nrm1, {0, bb, cc}/Norm[{bb, cc}]], bb == 0,
nrm1 = {0, 1, 0};
nrm2 = Cross[nrm1, {aa, 0, cc}/Norm[{aa, cc}]], cc == 0,
nrm1 = {0, 0, 1};
nrm2 = Cross[nrm1, {aa, bb, 0}/Norm[{aa, bb}]], True,
nrm1 = {-(((bb + cc)*Abs[aa])/(aa*Sqrt[2*aa^2 + (bb + cc)^2])),
Abs[aa]/Sqrt[2*aa^2 + (bb + cc)^2],
Abs[aa]/Sqrt[2*aa^2 + (bb + cc)^2]};
nrm2 = {((bb - cc)*Abs[aa])/Sqrt[2*aa^4 + (bb + cc)^2*(bb^2 + cc^2) +
aa^2*(3*bb^2 + 2*bb*cc + 3*cc^2)], -(((aa^2 + cc*(bb + cc))*
Abs[aa])/(aa*Sqrt[2*aa^4 + (bb + cc)^2*(bb^2 + cc^2) +
aa^2*(3*bb^2 + 2*bb*cc + 3*cc^2)])), ((aa^2 +
bb*(bb + cc))*Abs[aa])/(aa*Sqrt[2*aa^4 + (bb + cc)^2*(bb^2 + cc^2) +
aa^2*(3*bb^2 + 2*bb*cc + 3*cc^2)])}
];
(* la cabeza es un porcentaje 'hdsz' del segmento pt1 - pt2 *)
hdsz = porc;
hdrad = Sqrt[((pt2 - (hdsz pt1 + (1 - hdsz)pt2)).(pt2 - (hdsz pt1 +
(1 -hdsz)pt2)))]/5;
circ1[ttt_] := hdrad nrm1 Cos[ttt] +
hdrad nrm2 Sin[ttt] + (hdsz pt1 + (1 - hdsz)pt2);
circ2[ttt_] := (hdvec = pt2 + hdsz[[1]] (pt1 - pt2)/Norm[(pt1 - pt2)];
hdrad nrm1 Cos[ttt] + hdrad nrm2 Sin[ttt] + hdvec);
(* dx es número de lados del cono, Pi/nlds da 2nlds lados*)
dx = Pi/nlds;
pts = Partition[N[Table[circ1[t], {t, 0, 2 Pi, dx}]], 2, 1];
(*Solo fin de Flecha*)
arrowpolys =Map[{EdgeForm[], SurfaceColor[color],
Polygon[Flatten[{#, {pt2}}, 1]]} &, pts];
Return[arrowpolys];);
|
Una vez que tenemos una función para graficar flechas 3D, podemos crear una función sencilla para
los ejes 3D.
tira[str_] = StyleForm[str, FontSize -> 14];
Ejes3D[xmin_, xmax_, ymin_, ymax_, zmin_, zmax_] := {
(*Flechas*)
Flecha3D[{xmin, 0, 0}, {xmax, 0, 0}, 3, 0.08, GrayLevel[0]],
Flecha3D[{0, ymin, 0}, {0, ymax, 0}, 3, 0.09, GrayLevel[0]],
Flecha3D[{0, 0, zmin}, {0, 0, zmax}, 3, 0.09, GrayLevel[0]],
(*Ejes*)
GrayLevel[0],
Line[{{xmin, 0, 0}, {xmax, 0, 0}, {0, 0, 0}, {0, ymin, 0}, {0, ymax,
0}, {0, 0, 0}, {0, 0, zmin}, {0, 0, zmax}}],
Text[tira["X"], {xmax, -0.3, 0}],
Text[tira["Y"], {-0.3, ymax, 0.1}],
Text[tira["Z"], {0, -0.2, zmax}],
(* numeros *)
Table[Text[tira[i], {i, -0.3, 0.1}], {i, 1, xmax - 1}],
Table[Text[tira[i], {-0.3, i, 0.1}], {i, 1, ymax - 1}],
Table[Text[tira[i], {-0.3, 0.1, i}], {i, 1, zmax - 1}],
(* rayitas *)
Table[Line[{{-0.1, i, 0}, {0, i, 0}}], {i, ymax - 1}],
Table[Line[{{i, -0.1, 0}, {i, 0, 0}}], {i, xmax - 1}],
Table[Line[{{0, -0.1, i}, {0, 0, i}}], {i, zmin, zmax - 1}]
};
|
EJEMPLO
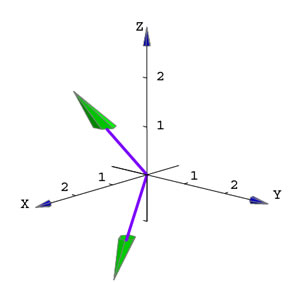
Como ejemplo, vamos a graficar un sistema de ejes y dos vectores. Usamos la función ve[pto1, pto2]
para graficar el segmento de pto1 a pto2 como un vector.
Figura 7.
El código es
color=RGBColor[0, 0.50, 0];
ve[{a1_, a2_, a3_}, {b1_, b2_, b3_}] = {
RGBColor[0.50, 0, 1],
(*Grosor de la linea*)
AbsoluteThickness[2],
(*Linea de pto1 a pto2*)
Line[{{a1, a2, a3}, {b1, b2, b3}}],
(*cabeza de la flecha*)
Flecha3D[{a1, a2, a3}, {b1, b2, b3}, 3, 0.4,color]
};
P = {0, 0, 0}; Q = {1, 0, -2}; R = {2, 0, 2};
g = Graphics3D[{
Ejes3D[-1, 3, -1, 3, -1, 3],
ve[P, Q],
ve[P, R]
}, Boxed -> False,
AmbientLight -> RGBColor[1, 1, 0],
ViewPoint -> {2.426, 2.190, 0.878}];
Show[g];
|
Nota: Una versión de flecha 3D más sencilla, implementada por Tom Wickham-Jones,
se muestra en el código siguiente
Options[Arrow3D] = {HeadLength -> 0.3, HeadNormal -> {0, 0, 1},HeadWidth -> 0.5};
Arrow3D[a_,b_,opts___]:=
Module[{abLength=N[Sqrt[(b-a).(b-a)]],abUnit,headPerp,headPerpLength,
headLength,headNormal, headWidth},
{headLength,
headNormal,
headWidth}={HeadLength,HeadNormal,HeadWidth}/.{opts}/.Options[Arrow3D];
abUnit=(b-a)/abLength;
headPerp=Cross[abUnit,N[headNormal]];
headPerp=headPerp/Sqrt[N[headPerp.headPerp]];
{Line[{a,b-abUnit*headLength}],
Polygon[{b,b-abUnit*headLength+headPerp*headWidth/2*headLength,
b-abUnit*headLength,
b-abUnit*headLength-headPerp*headWidth/2*headLength}]}];
|
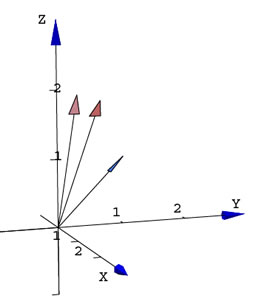
Veamos un ejemplo
g = Graphics3D[{
Ejes3D[-1, 3, -1, 3, -1, 3],
Arrow3D[P, Q],
Arrow3D[P, R],
Arrow3D[{0, 0, 0}, {1, 1, 1}]
}, Boxed -> False,
ViewPoint -> {2.426, 2.190, 0.878}] //Show
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|