En las secciones anteriores se vieron métodos generales para implementar
superficies de cualquier tipo, usando mayormente primitivas. DrawGraphics y CurvesGraphics ofrecen nuevas
herramientas para los casos generales y también para casos particulares.
DrawGraphics es un paradigma alternativo para producir gráficos en Mathematica.
Las rutinas básicas de DrawGraphics producen los gráficos de Mathematica, sin desplegarlos,
y extraen las primitivas del objeto producido por Mathematica para poder combinar diferentes elementos gráficos
en un solo contexto.
DrawGraphics y CurvesGraphics son paquetes que extraen las primitivas de los gráficos
y los combinan para producir gráficos con un código más natural.
CurvesGraphics funciona usando DrawGraphics y extiende los comandos para curvas orientadas.
Instalación
Se Podría copiar la carpeta DrawGraphics y el archivo
CurvesGraphics.m en el directorio
C:\...\Wolfram Research\Mathematica\5.0\AddOns\Applications
Para llamar a ambos paquetes se ejecuta el código
Needs["DrawGraphics`DrawingMaster`"];
Needs["CurvesGraphics`"];
Comandos básicos
Los nombres de los comandos en DrawGraphics, son similares a los de Mathematica,
solo se agrega 'Draw'. Por ejemplo
| Mathematica
|
|
DrawGraphics |
| ParametricPlot3D |
|
ParametricDraw3D |
| Plot3D |
|
Draw3D |
| Show |
|
Draw3DItems |
| InequalityPlot3D |
|
InequalitDraw3D |
Las rutinas 'Draw' tienen la misma forma y aceptan las mismas opciones que las rutinas 'Plot' excepto
las opciones AspectRatio, Frame, PlotLabel, etc. que no producen ningún efecto.
Algunos comandos de Mathematica no están presentes en los paquetes, pero se pueden incorporar como se
verá más adelante. También hay comandos nuevos en estos paquetes.
A través de los ejemplos que siguen, vamos a mostrar algunas de las calidades de este nuevo paradigma,
aplicándolo a los
ejemplos anteriores y a otros ejemplos nuevos
La documentación de DrawGraphics viene incluida en la carpeta DrawGraphics, ([12]) . Un manual actualizado de CurvesGraphics
se puede obtener en ([12])
Ejemplos
- Ejes 3D
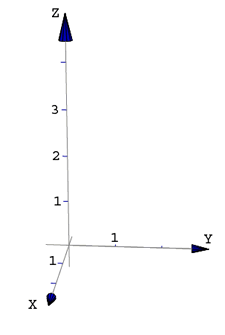
Podemos hacer un comando que dibuje un sistema de ejes 3D usando el comando ArrowLine3D de DrawGraphics.
También podemos usar Arrow3D para aplicarlo a curvas. La sintaxis es
Arrow3D[base,cabeza, opciones]
ArrowLine3D[ puntos,opciones...]
|
ArrowLine3D recibe una lista puntos = {pt1, pt2,...,ptk}
La opción 'HeadSegments3D' especifica el número de segmentos
triángulares usados para dibujar el cono de la flecha.
El default es 10. Una flecha plana se logra con 2.
flechas1 = Draw3DItems[{Arrow3D[{0, 0, 0}, {0, 1, 1}],
RGBColor[0, 0, 1],
Arrow3D[{0, 0, 0}, {1, 0, 1}],
RGBColor[0.5, 0, 1],
AbsoluteThickness[2],
SurfaceColor[RGBColor[0, 1, 0]],
Arrow3D[{0, 0, 0}, {1, 1, 0}]
},
ViewPoint -> {2.209, 2.115, 1.449},
Boxed -> False,
PlotRange -> All];
|
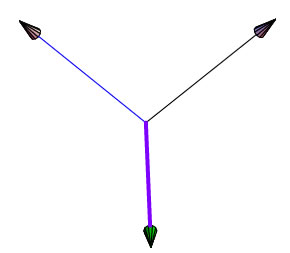
Figura 22.
SetOptions[Arrow3D, HeadSegments3D -> 2];
flechas2 = Draw3DItems[{Arrow3D[{0, 0, 0}, {0, 1, 1}],
RGBColor[0, 0, 1],
Arrow3D[{0, 0, 0}, {1, 0, 1}]
},
ViewPoint -> {2.209, 2.115, 1.449},
Boxed -> False,
PlotRange -> All];
|
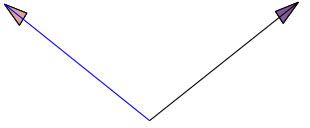
- Ejes 3D
Usamos un código similar al visto más arriba
Ejes[xmin_, xmax_, ymin_, ymax_, zmin_, zmax_] := {
(*Flechas*)
SurfaceColor[RGBColor[0, 0, 1]],
ArrowLine3D[{{xmin, 0, 0}, {0, 0, 0}, {xmax, 0, 0}}],
ArrowLine3D[{{0, ymin, 0}, {0, 0, 0}, {0, ymax, 0}}],
ArrowLine3D[{{0, 0, zmin}, {0, 0, 0}, {0, 0, zmax}}],
GrayLevel[0],
Text["X", {xmax, -0.3, 0}],
Text["Y", {-0.3, ymax, 0.1}],
Text["Z", {0, -0.2, zmax}],
(* numeros *)
Table[Text[i, {i, -0.3, 0}], {i, 1, xmax - 2, 1}],
Table[Text[i, {-0.3, i, 0}], {i, 1, ymax - 2, 1}],
Table[Text[i, {-0.3, -0.3, i}], {i, 1, zmax - 2, 1}],
RGBColor[0, 0, 0.627451],
(* rayitas *)
Table[Line[{{-0.1, i, 0}, {0, i, 0}}], {i, 1, ymax - 1, 1}],
Table[Line[{{i, -0.1, 0}, {i, 0, 0}}], {i, 1, xmax - 1, 1}],
Table[Line[{{0, -0.1, i}, {0, 0, i}}], {i, 1, zmax - 1, 1}]
};
SetOptions[Arrow3D, HeadSegments3D -> 10];
elGraf = Draw3DItems[{
GrayLevel[0.501961],
Ejes[-0.5, 3, -0.5, 3, -0.5, 5]},
ViewPoint -> {3.221, 0.246, 1.008
},
Boxed -> False,
PlotRange -> All];
|
- Usando JavaView
Procedemos como se indicó más arriba.
Primero ejecutamos el código
Needs["JLink`"];
InstallJava[];
<< JavaView`JLink`
viewer = InstallJavaView[];
y luego ya podemos levantar la ventana de JavaView
JavaView[elGraf];
- 'RealTime3D'
'RealTime3D' nos permite interactuar con el gráfico directamente en el 'notebook'.
Se ejecuta el código (para usar 'RealTime3D' se debió eliminar StyleForm[] de Ejes[...])
<< RealTime3D`
Show[elGraf];
<< Default3D`
- Draw3D
Veamos un ejemplo de cómo usar Draw3DItems y Draw3D
plot1 = Draw3DItems[{
Ejes2[-0.5, 3, -0.5, 3, -0.5, 9],
Draw3D[x^2 + y^2, {x, 0, 3}, {y, 0, 3},
PlotPoints -> 20] //UseWireFrame,
Draw3D[y + 6, {x, -1, 3}, {y, -1, 3}]
},
Boxed -> False,
ViewPoint -> {1.324, -2.001, 2.386},
ImageSize -> 100];
|
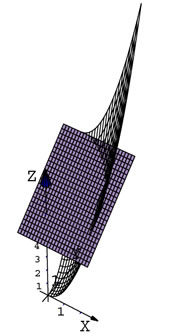
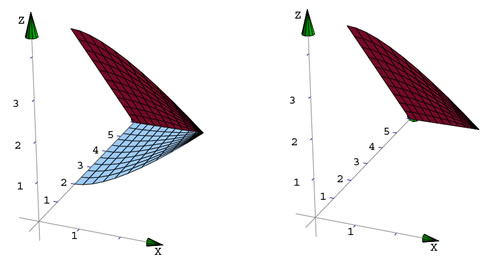
- ParametricDraw3D
Veamos un ejemplo de cómo usar ParametricDraw3D
plot2 = Draw3DItems[{EdgeForm[],
Ejes2[-0.5, 3, -0.5, 3, -0.5, 9],
SurfaceColor[RGBColor[0, 1, 0]],
ParametricDraw3D[{r*Cos[t], r*Sin[t], r^2},
{r, 0, 3}, {t,0, Pi/2}]
},
ViewPoint -> {0.636, -2.991, 1.449},
Boxed -> False
];
|
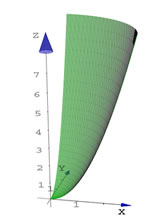
Figura 26.
- LinearClipPlot3D
LinearClipPlot3D es un comando de 'CurvesGraphics' que dibuja el recorte de una superficies
usando planos vía desigualdades lineales
LinearClipPlot3D[3DSurface, LinearInequality, variables]
Por ejemplo, observemos todos los gráficos que produce el siguiente código
paraboloid = ParametricPlot3D[r{Cos[t], Sin[t], r}, {r, 0, 3}, {t, 0, 2*Pi}];
GInt1 = LinearClipPlot3D[paraboloid, z <= y + x + 1 , x, y, z];
(*Como GInt1 es Graphics3D[{primitivas}] entonces GInt1[[1]] = {primitivas} *)
intersecciones = Graphics3D[{Join[{EdgeForm[]}, GInt1[[1]]]}];
Show[intersecciones]
|
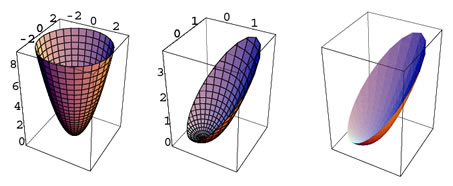
Figura 27.
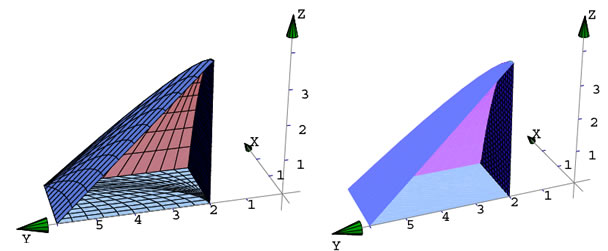
- Sólido usando LinearClipPlot3D
Vamos a usar LinearClipPlot3D para ayudarnos a implementar el sólido limitado por
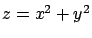 y los planos y los planos 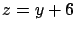 y y 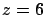 , en el primer octante. Observe que este comando solo
funciona con desigualdades lineales. , en el primer octante. Observe que este comando solo
funciona con desigualdades lineales.
paraboloid2 =ParametricPlot3D[r{Cos[t], Sin[t], r},
{r, 0, 3}, {t, 0, Pi/2},
PlotPoints -> 40];
ejes = Graphics3D[Ejes2[-0.5, 3, -0.5, 3, -0.5, 9]];
GInt1 = LinearClipPlot3D[paraboloid2, 6 <= z <= y + 6 , x, y, z];
(*GInt1 es Graphics3D[{primitivas}] entonces GInt1[[1]] = {primitivas} *)
intersecciones = Graphics3D[{Join[{EdgeForm[]}, GInt1[[1]]]}];
(*---------------- plano 1 ---------------------------------*)
z2[y_] = {Sqrt[6 + y - y^2], y, 6 + y};
z1[y_] = {0, y, 6 + y};
dx = 0.1;
Rplano1 = Table[Polygon[{z1[i], z1[i + dx], z2[i + dx], z2[i], z1[i]
}], {i, 0, 2.7, 0.1}];
dx = 0.01;
Rplano2 = Table[Polygon[{z1[i], z1[i + dx], z2[i + dx], z2[i], z1[i]
}], {i, 2.7, 3 - 0.01, 0.01}];
(*---------------- plano 2 ----------------------------------*)
dt = (Pi/2)/30;
z6[te_] = {Sqrt[6]Cos[te], Sqrt[6]*Sin[te], 6 };
Rplanoz6 = Table[
Polygon[{
z6[i], z6[i + dt], {0, 0, 6}, z6[i]
}],
{i, 0, Pi/2 - dt, dt}];
planos = Graphics3D[{
{EdgeForm[],
SurfaceColor[RGBColor[0, 1, 0]],
Rplano1, Rplano2,
SurfaceColor[RGBColor[1, 1, 0.501961]],
Rplanoz6}
}];
plot4 = Show[{
ejes, planos, intersecciones
}, ViewPoint -> {2.894, -0.892, 1.510},
Boxed -> False,
PlotRange -> All]
|
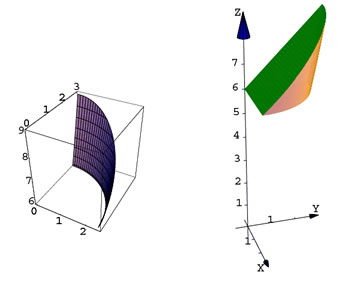
- InequalityDraw3D
Esta rutina es muy conveniente para dibujar sectores de superficies y sólidos. Vamos a ver algunos ejemplos de su uso.
-
Sector del plano 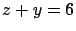 al ser cortado por la superficie al ser cortado por la superficie 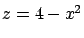 con x ≤ 2, en el primer octante. con x ≤ 2, en el primer octante.
La idea es definir la región de la proyección del plano, en XY, con una desigualdad. InequalityDraw3D
toma esta región, definida por una desigualdad, y la proyecta sobre el plano que también debe ser definido
por otra desigualdad. El código generado por InequalityDraw3D incluye los polígonos de la proyección
y el sector del plano. Para eliminar la proyección del gráfico, extraemos los polígonos del sector del plano
En el siguiente código se muestra el procedimiento
(*región de proyección en XY: y >= 2 +
x^2, {x,0, 2}, {y, 2, 6} *)
eqns3 = y >= 2 + x^2 ∧ y ≤ 6 - z;
(regionP = InequalityDraw3D[
eqns3, {x,0, 2}, {y, 2, 6}, {z, 0, 4},
PlotPoints -> 10];)
elGraf = Draw3DItems[
{
GrayLevel[0.501961],
Ejes[-0.5, 3, -0.5, 7, -0.5, 5],
regionP[[1,1]]
(*sin los polígonos de la proyección*)
},
ViewPoint -> {1.125, 2.903, 1.325},
Boxed -> False,
PlotRange -> All
];
|
-
Sólido limitado por los planos 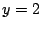 , , 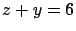 y la superficie y la superficie 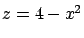 , en el primer octante. , en el primer octante.
En este caso si nos interesa la proyección pues es parte del sólido. En la siguiente implementación
se omite la pared en YZ para efectos de visualizar el interior.
En el siguiente código se nuestra el procedimiento
eqns2 = z ≤ 4 - x^2 ∧ y ≤ 6 - z;
(region=InequalityDraw3D[eqns2, {x, 0, 2}, {y, 2, 6}, {z, 0, 4},
PlotPoints -> 10];)
(*agregamos EdgeForm[] para ocultar la malla*)
region = Join[{EdgeForm[]}, region];
(*la pared en y=2 va de z=0 hasta z=4 - x^2 *)
zt[x_, vz_] = If[vz <= 4 - x^2, vz, 4 - x^2];
elGraf2 = Draw3DItems[
{
GrayLevel[0.501961],
Ejes[-0.5, 3, -0.5,
7, -0.5, 5],
region,
ParametricDraw3D[{x, 2, zt[x, vz]}, {x, 0, 2}, {vz, 0, 4}]
},
ViewPoint -> {-2.815,
1.118, 1.510},
AmbientLight ->
RGBColor[0, 0, 0.627451],
Boxed -> False,
PlotRange -> All
];
|
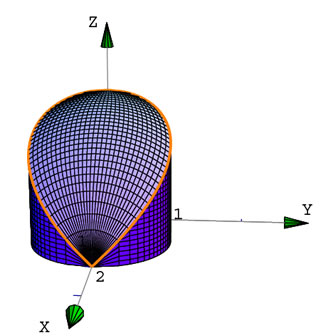
-
Sólido que corresponde a la región interior de la esfera 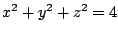 y al interior del cilindro y al interior del cilindro
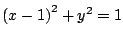 , en el primer octante. , en el primer octante.
En este caso la proyeción sobre XY es la proyección del cilindro
En el siguiente código se muestra el procedimiento
(*Curva intersección : Cint[x_] = {x, ħSqrt[1 - (x - 1)^2],
Sqrt[4 - 2 x] *)
(* cilindro = {x, ħSqrt[1 - (x - 1)^2], cz[x, z]} *)
cz[x_, tz_] = If[tz ≤ Sqrt[4 - 2 x], tz, Sqrt[4 - 2 x]];
cil1[x_, tz_] = {x, Sqrt[1 - (x - 1)^2], cz[x, tz]};
cil2[x_, tz_] = {x, -Sqrt[1 - (x - 1)^2], cz[x, tz]};
Cint1[x_] = {x, Sqrt[1 - (x - 1)^2], Sqrt[4 - 2 x]};
Cint2[x_] = {x, -Sqrt[1 - (x - 1)^2], Sqrt[4 - 2 x]};
eqns1 = (x - 1)^2 + y^2 ≤ 1 ∧ x^2 + y^2 + z^2 ≤ 4;
regionEsfera = InequalityDraw3D[ eqns1, {x, 0, 2}, {y, -1, 1},
{z, 0, 2},
PlotPoints
-> 30];
elGraf = Draw3DItems[
{
GrayLevel[0.501961],
Ejes[-0.5, 4, -0.5, 3, -0.5, 3],
regionEsfera,
(*
cilindro, de z=0 hasta la curva de intersección*)
SurfaceColor[RGBColor[0.501961, 0, 1]],
ParametricDraw3D[cil1[x, z], {x, 0, 2}, {z, 0, 2}],
ParametricDraw3D[cil2[x, z], {x, 0, 2}, {z, 0, 2}],
AbsoluteThickness[1.5],
RGBColor[1, 0.501961, 0],
ParametricDraw3D[Cint1[t], {t, 0, 2}],
ParametricDraw3D[Cint2[t], {t, 0, 2}]
},
ViewPoint -> {3.221, 0.246, 1.008},
Boxed -> False,
AmbientLight -> RGBColor[0, 0, 1],
PlotRange -> All
];
|
-
De nuevo el Sólido 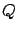 limitado por el paraboloide limitado por el paraboloide 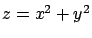 el plano el plano 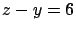 , en el primer octante. Compare con el sólido en la
sección anterior , en el primer octante. Compare con el sólido en la
sección anterior
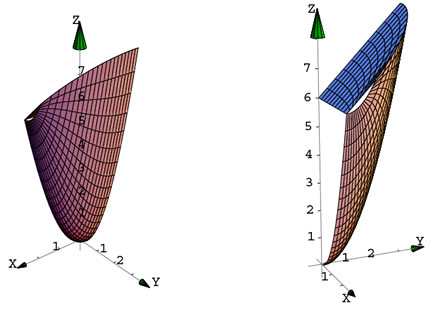
Figura 32.
Para la implementación, de nuevo,
proyectamos sobre XY. El código es como sigue
eqns4 = x^2 + (y - 1/2)^2 ≤ 25/4 ∧ z ≤ x^2 + y^2 ∧ z ≤ 6 + y
;
regionParaboloide=InequalityDraw3D[eqns4, {x, 0, Sqrt[6]}, {y,
0, 3}, {z, 0, 9},
PlotPoints -> 20];
eqns5 = x^2 + (y - 1/2)^2 ≤ 25/4 ∧ z ≤ 6 + y ;
(regionPlano = InequalityDraw3D[ eqns5, {x, 0, Sqrt[6]}, {y, 0,
3}, {z, 0,
9},
PlotPoints -> 10];)
elGraf = Draw3DItems[
{
GrayLevel[0.501961],
Ejes[-0.5, 3, -0.5, 4, -0.5, 9],
regionParaboloide[[1, 1]],
regionPlano[[1, 1]]
},
ViewPoint -> {2.962, -1.337, 0.943},
Boxed -> False,
PlotRange -> All
];
|
-
Disco
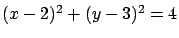 sobre el plano sobre el plano
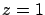 . .
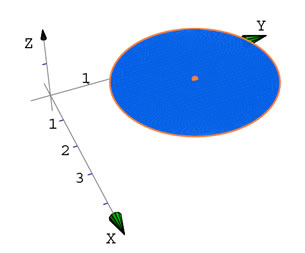
Figura 33.
El código es como sigue
eqns6 = (x - 2)^2 + (y - 3)^2 ≤ 4 ∧ z <= 1 ;
regionC = InequalityDraw3D[ eqns6, {x, 0, 4}, {y, 1, 5}, {z, 0, 1},
PlotPoints -> 35];
regionC = Join[{EdgeForm[]}, regionC[[1,1]]];
elGraf = Draw3DItems[
{
GrayLevel[0.501961],
Ejes[-0.5, 5, -0.5, 6,
-0.5, 2],
SurfaceColor[RGBColor[0,
0.501961, 1]],
regionC,
AbsoluteThickness[1],
RGBColor[1, 0.501961,
0.25098],
ParametricDraw3D[{2 + 2*Cos[t],
3 + 2*Sin[t], 1}, {t, 0, 2Pi}],
AbsolutePointSize[4],
Point[{2, 3, 1}]
},
ViewPoint -> {2.354,
-1.062, 2.186},
Boxed -> False,
PlotRange -> All
];
|
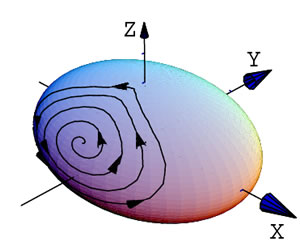
- PlotCurveOnSurface3D: curvas sobre una supeficie
En Mathematica las curvas sobre objetos gráficos no se ven, en general, muy bien.
Esto se resuelve en CurvesGraphics con PlotCurveOnSurface3D.
En el siguiente ejemplo se dibuja una curva sobre una superficie. Se habilita la orientación a la curva
con la opción 'Oriented -> True'
plot5 = PlotCurveOnSurface3D[
{{4Cos[u]Cos[v], 3Sin[u]Cos[v], 2Sin[v]},
{u, 0,2Pi}, {v, -Pi/2, Pi/2},
PlotPoints -> {51, 41}},
{{t*Cos[30t] - Pi/2, t*Sin[30t] + Pi/6},
{t, 0, 1}, Oriented -> True,
PlotPoints
-> 100},
Ticks -> None,
Boxed -> False,
Axes -> False];
ejes = Graphics3D[Ejes2[-5, 6, -5, 6, -0.5, 4]];
Show[{ejes, plot5},
ViewPoint -> {2.021, -2.077, 1.747},
Boxed -> False,
PlotRange -> All]
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|