Vamos a describir como se puede implementar un trozo de superficie (que no
es necesariamente generada por una curva) usando su proyección. La idea es observar
una manera de implementar un gráfico con el próposito de usar métodos similares para otros tipos de superficies
que no son accesibles directamente con las herramientas implementadas en Mathematica .
EJEMPLO
Consideremos el problema de dibujar el sólido  limitado por el paraboloide limitado por el paraboloide 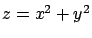 el plano el plano 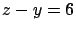 , en el primer octante. , en el primer octante.
Figura 18
Para implementar este gráfico debemos implementar cada una de sus partes por separado
- Paraboloide.
En
el caso de este sector de paraboloide, una idea para su
implementación es hacer una especie de
abanico con vértice en la parte más alta, como se
muestra en la figura que sigue.
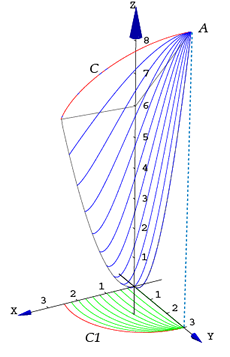
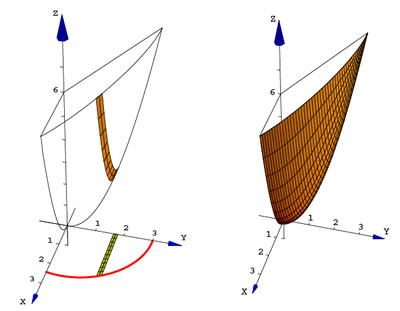
Figura 19.
La curva 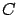 se proyecta en la curva se proyecta en la curva 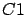 ; las trazas
que conforman el abanico son una deformación de la
curva ; las trazas
que conforman el abanico son una deformación de la
curva 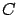 y por tanto, las curvas de nivel
correspondientes son una deformación de la curva y por tanto, las curvas de nivel
correspondientes son una deformación de la curva
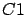
Bien, vamos a hacer el tejido de polígonos en la región de proyección del trozo de paraboloide,
en el plano 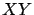 ,
y luego proyectar estos polígonos al paraboloide. ,
y luego proyectar estos polígonos al paraboloide.
Para hacer este tejido, vamos a tomar la curva 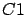 y deformarla, multiplicando su coordenada y deformarla, multiplicando su coordenada 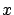 por un parámetro que toma valores entre
por un parámetro que toma valores entre 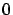 y y 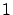 . Esto produce un conjunto de curvas, todas con
el mismo número de puntos.
Luego, formamos los polígonos de la telaraña uniendo cada par de puntos de una curva . Esto produce un conjunto de curvas, todas con
el mismo número de puntos.
Luego, formamos los polígonos de la telaraña uniendo cada par de puntos de una curva 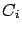 con el respectivo par de puntos en la curva siguiente con el respectivo par de puntos en la curva siguiente
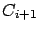 . Luego esta 'telaraña' la proyectaremos al paraboloide. . Luego esta 'telaraña' la proyectaremos al paraboloide.
La curva 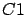 de intersección entre el plano de intersección entre el plano 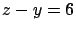 con el paraboloide con el paraboloide 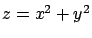 , proyectada en el plano , proyectada en el plano 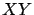 ,
tiene ecuación ,
tiene ecuación
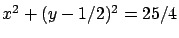 , o sea, un círculo de radio , o sea, un círculo de radio 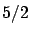 .
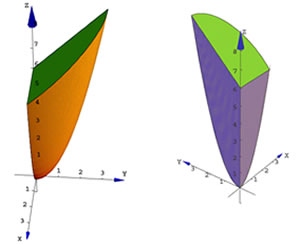
Su parametrización (en el primer octante) en el plano .
Su parametrización (en el primer octante) en el plano 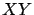 es
es
Para obtener una familia de curvas a partir de 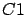 , usamos la función , usamos la función
f[ra_, t_, s_] = {s*ra*Cos[t], 1/2 + ra*Sin[t], 0}, (* s en [0,1] *)
y la familia de curvas 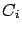 se genera con se genera con
f[ra_, t_, s_] = {s*ra*Cos[t], 1/2 + ra*Sin[t], 0}, (* s en [0,1] *)
angIni = -0.201358;
dt = (-angIni + Pi/2)/50; (*de angIni a Pi/2 en 50 pasos*)
curvas = Table[f[5/2, i, j], {j, 0, 1, 0.1}, {i, angIni, Pi/2, dt}];
(*dt no ajusta bien, asi que agregamos la ultima curva *)
AppendTo[curvas, Table[{5/2*Cos[t], 1/2 + 5/2*Sin[t], 0}, {t, angIni, Pi/2, dt}]];
|
Las curvas y la 'telaraña' se muestran en las siguientes figuras, junto con el código necesario
(*numero curvas nc*)
nc = Length[curvas];
(*todas las curvas tienen np puntos*)
np = Length[curvas[[1]]];
curvaC = Line[curvas[[nc]]];
(*curvas ci*)
netC = Table[Line[curvas[[ci]]], {ci, 1, nc - 1}];
(* cada poligono esta formado por dos puntos en la curva ci
curvas[[ci, pi]], curvas[[ci, pi+1]]
y dos puntos en la curva ci+1
curvas[[ci + 1, pi]], curvas[[ci + 1, pi + 1]], *)
netP = Table[Polygon[{curvas[[ci, pi]],
curvas[[ci + 1, pi]],
curvas[[ci + 1, pi + 1]],
curvas[[ci, pi + 1]],
curvas[[ci, pi]]
}], {pi, 1, np - 1}, {ci, 1,nc - 1}];
g = Graphics3D[{ Ejes3D[-1, 4, -1, 4, -0.1, 3],
netP,
RGBColor[1, 0, 0],
AbsoluteThickness[2],
curvaC
}, Boxed -> False,
ViewPoint -> {2.580, 1.056, 1.918}
];
Show[g];
|
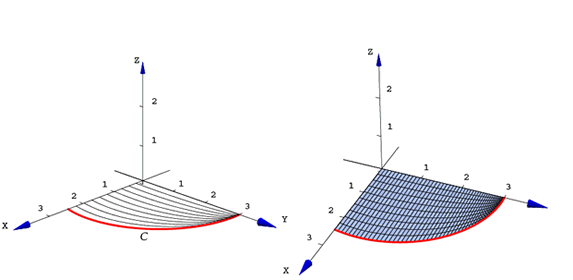
Figura 19.
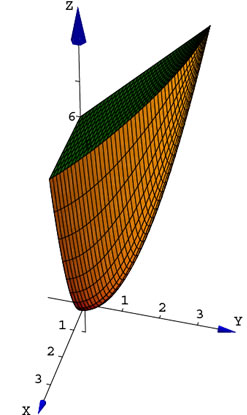
Luego, cada polígono es proyectado sobre el paraboloide, para hacer esto, redefinimos la función
f[ra_, t_, s_]
f[ra_, t_, s_] = {s*ra*Cos[t],1/2 + ra*Sin[t], (s*ra*Cos[t])^2 + (1/2 + ra*Sin[t])^2};
corteParaboloide = Table[Polygon[{ curvas[[ci, pi]],
curvas[[ci + 1, pi]],
curvas[[ci + 1, pi + 1]],
curvas[[ci, pi + 1]],
curvas[[ci, pi]]
}], {pi, 1, np - 1}, {ci, 1,nc - 1}];
g = Graphics3D[{ Ejes3D[-1, 4, -1, 4, -1, 9],
SurfaceColor[RGBColor[1, 1, 0]],
corteParaboloide
}, Boxed -> False,
ViewPoint -> {2.493, 0.673, 2.186}
];
Show[g];
|
Figura 20.
- El plano
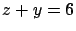
Ya que en este caso el plano comparte la proyección sobre, el plano 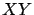 , con el paraboloide,
podemos aprovechar la construcción del paraboloide para construir el plano.
Nada más se debe modificar la coordenada 'z' de la función f[ra_, t_, s_]. Agregamos el siguiente código , con el paraboloide,
podemos aprovechar la construcción del paraboloide para construir el plano.
Nada más se debe modificar la coordenada 'z' de la función f[ra_, t_, s_]. Agregamos el siguiente código
f[ra_, t_, s_] = {s *ra*Cos[t], 1/2 + ra*Sin[t], 6 + 1/2 + ra*Sin[t]};
curvas = Table[f[5/2, i, j], {j, 0, 1, 0.1}, {i, angIni, Pi/2, dt}];
AppendTo[curvas,
Table[{5/2*Cos[t],
1/2 + 5/2*Sin[t],
(5/2*Cos[t])^2 + (1/2 + 5/2*Sin[t])^2},
{t, angIni, Pi/2, dt}]];
planoT = Table[Polygon[{curvas[[ci, pi]],
curvas[[ci + 1, pi]],
curvas[[ci + 1, pi + 1]],
curvas[[ci, pi + 1]],
curvas[[ci, pi]]
}], {pi, 1, np - 1}, {ci, 1,nc - 1}];
g = Graphics3D[{ Ejes3D[-1, 4, -1, 4, -1, 9],
SurfaceColor[RGBColor[1, 1, 0]],
corteParaboloide,
SurfaceColor[RGBColor[0.501961, 1, 0]],
planoT
}, Boxed -> False,
ViewPoint -> {2.493, 0.673, 2.186}
];
Show[g];
|
Figura 21.
- Los planos laterales,en los planos
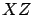 y y 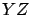 , son más sencillos. En el plano , son más sencillos. En el plano 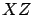 , el plano va de la curva , el plano va de la curva
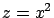 hasta la curva hasta la curva 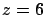 y en el plano y en el plano 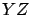 el plano va de la curva el plano va de la curva
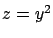 hasta la curva hasta la curva 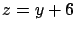 . Simplemente hacemos una grupo de polígonos desde la curva de abajo
hasta la curva de arriba. En el código que se agrega, se incluyen los bordes (curvas) del sólido. . Simplemente hacemos una grupo de polígonos desde la curva de abajo
hasta la curva de arriba. En el código que se agrega, se incluyen los bordes (curvas) del sólido.
(*-------------bordes ----------------*)
cxz = Line[Table[{t, 0, t^2}, {t, 0, Sqrt[6], 0.1}]];
cyz = Line[Table[{0, t, t^2}, {t, 0, 3, 0.1}]];
cpl1 =Line[Table[{5/2*Cos[t],
1/2 + 5/2*Sin[t],
(5/2*Cos[t])^2 + (1/2 + 5/2*Sin[t])^2}
,{t,angIni, Pi/2, dt}]];
cpl2 = Line[{{Sqrt[6], 0, 6}, {0, 0, 6}, {0, 3, 9}}];
(*-------------paredes------------------*)
c2[y1_] = {0, y1, 6 + y1};
c1[y1_] = {0, y1, y1^2};
di = 0.1;
paredyz =Table[Polygon[{c1[i], c1[i + di],
c2[i + di], c2[i], c1[i]}]
,{i, 0,3 - di, di}];
c2[x1_] = {x1, 0, 6};
c1[x1_] = {x1, 0, x1^2};
paredxz =Table[Polygon[{c1[i], c1[i + di], c2[i + di], c2[i], c1[i]}]
,{i, 0,Sqrt[6], di}];
g = Graphics3D[{ Ejes3D[-1, 4, -1, 4, -1, 9],
SurfaceColor[RGBColor[1, 1, 0]],
corteParaboloide,
SurfaceColor[RGBColor[0.501961, 1, 0]],
planoT,
SurfaceColor[RGBColor[0.501961, 0.501961, 1]],
paredyz, paredxz,
cxz, cyz, cplano1, cplano2
}, Boxed -> False,
ViewPoint -> {2.493, 0.673, 2.186}
];
Show[g];
|
-
Como un ejemplo curioso, presentamos una implementación de la botella de Klein [15]

Figura 22.
Fue generada con este código [15]
color = RGBColor[0, 0, 0.627451];
bot = {(2.5 + 1.5 Cos[v]) Cos[u], (2.5 + 1.5 Cos[v]) Sin[u], -2.5
Sin[v], EdgeForm[]};
mid = {(2.5 + 1.5 Cos[v]) Cos[u], (2.5 + 1.5 Cos[v]) Sin[u], 3v,
EdgeForm[]};
han = {2 - 2 Cos[v] + Sin[u], Cos[u], 3v, EdgeForm[]};
top = {2 + (2 + Cos[u]) Cos[v], Sin[u], 3Pi + (2 + Cos[u]) Sin[v],
EdgeForm[]};
bottom = ParametricPlot3D[bot, {u, 0, 2Pi}, {v, 0, Pi}, PlotPoints
-> {32, 16}
,AmbientLight -> color, Boxed -> False, Axes -> False];
middle = ParametricPlot3D[mid, {u, 0, 2Pi}, {v, 0, Pi}, PlotPoints
-> {32, 16},
AmbientLight -> color, Boxed -> False, Axes -> False];
topper = ParametricPlot3D[top, {u, 0, 2Pi}, {v, 0, Pi}, PlotPoints
-> {32, 16}
,AmbientLight -> color, Boxed -> False, Axes -> False];
handle = ParametricPlot3D[han, {u, 0, 2Pi}, {v, 0, Pi},
PlotPoints -> {32, 16}, AmbientLight -> color,
Boxed -> False, Axes
->
False];
todo = Show[{handle, topper, middle, bottom}, Boxed -> False,
Axes -> False, AmbientLight -> color]
|
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|

![\begin{displaymath}C1: \; \; \left(\frac{5}{2}\,\mbox{cos}t, \frac{1}{2}+ \frac{...
...ight), \; \; \;
t \in \left[-0.201358,\; \frac{\pi}{2}\right] \end{displaymath}](img72.gif)