Parametrización de una curva en el espacio
La forma paramétrica de una curva en 2D o 3D o incluso de una
superficie, es fundamental a la hora de trazar su gráfica, como
veremos.
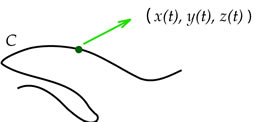
Figura 9.
Algunas parametrizaciones útiles, en dos dimensiones, son
- Segmento de recta que une
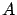 con con 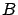 : :
![$(x,y,z)= A\,+\,t(B-A), \; \; \; t \, \in \,
[0,1]$](img21.gif)
- Círculo, en el plano
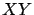 , de centro , de centro 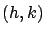 y radio y radio 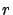 : :
![$(h+r\cos(t),
k+r\,\mbox{sen}(t),0),\; \; t \, \in \, [0, 2\pi]$](img25.gif)
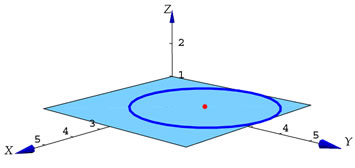
- Elipse
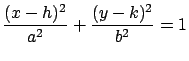 : :
![$(h+a\cos(t),
k+b\mbox{sen}(t),0),\; \; t \, \in \, [0, 2\pi]$](img27.gif)
- Hipérbola
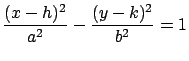 : :
![$(h+a \sec(t),
k+b\, \mbox{tan}(t),0), \; \; t \, \in \, [0, 2\pi]$](img29.gif)
- Para las curvas, en los planos
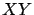 , , 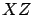 y y 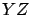 , con
ecuación funcional, se puede tomar la variable independiente
como parámetro. , con
ecuación funcional, se puede tomar la variable independiente
como parámetro.
EJEMPLO
Grafiquemos el círculo
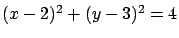 sobre el plano sobre el plano
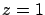 . .
 - Aunque podríamos usar ParametricPlot3D[] para graficar
el círculo, vamos a usar una lista de líneas para dibujar
esta curva.
Las líneas unen los puntos z(t) =
![$(2 + r*\mbox{cos}\, t,\; 3 + r*\mbox{sen} \,t,\; 1), \; \; t \in [0, 2\pi]$](img34.gif) .
Los puntos son igualmente espaciados. Usaremos 30 puntos, por lo que el paso podría ser dt .
Los puntos son igualmente espaciados. Usaremos 30 puntos, por lo que el paso podría ser dt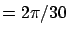 . .
Para hacer la lista de puntos usamos el comando Table[]
 - Para dibujar el plano
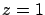 , es conveniente dibujar con
ParametricPlot3D[] para que la circunferencia no sea
parcialmente ocultada por un solo gran polígono. El paquete CurvesGraphics,
que veremos más adelante, ofrece una buena solución al problema de ocultamiento
de curvas sobre superficies. , es conveniente dibujar con
ParametricPlot3D[] para que la circunferencia no sea
parcialmente ocultada por un solo gran polígono. El paquete CurvesGraphics,
que veremos más adelante, ofrece una buena solución al problema de ocultamiento
de curvas sobre superficies.
El código es
r = 2; (*radio*)
nptos = 30; (*numero de puntos*)
dt = (2Pi -0)/nptos; (*paso*)
z[t_] = {2 + r*Cos[t], 3 + r*Sin[t], 1}; (*parametrizacion*)
circulo =Line[Table[z[tetha], {tetha, 0, 2Pi, dt}]];
Q = {5, 0, 1}; P = {0, 0, 1}; R = {0, 5, 1};
(* plano P + t*(Q - P) + s*(R - P)= {5 t, 5 s, 1 *)
planoz1 = ParametricPlot3D[{5 t, 5 s, 1, EdgeForm[]},
{t, 0, 1}, {s, 0, 1},
DisplayFunction -> Identity];
g = Graphics3D[{
Ejes3D[-1, 6, -1, 6, -1, 3],
GrayLevel[0.68],
AbsoluteThickness[2], (*Grosor de la linea*)
circulo,
AbsolutePointSize[4],
RGBColor[1, 0, 0],
Point[{2, 3, 1}]
}, Boxed -> False,
ViewPoint -> {2.426, 2.190, 0.878}];
graf = Show[{g, planoz1}, DisplayFunction -> \$DisplayFunction];
JavaView[graf];
|
NOTA: en el ejemplo anterior, se puede implementar el plano como un paralelogramo,
Q = 5, 0, 1; P = 0,0, 1; R = 0, 5, 1; S = (Q - P) + (R - P) + P;
planoz1 =Polygon[Q, P, R, S, Q];
En este caso, esto no es conveniente; la visibilidad del círculo se vería afectada
como se ve en la versión 1.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|

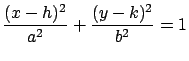 :
:
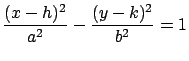 :
: