Gráficos 3D		Figueroa, G.  Mora, W..

  Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18 

 

Discos

EJEMPLO

Vamos ahora a recortar el círculo, es decir, vamos a dibujar el disco  $(x-2)^2+(y-3)^2=4$ sobre el plano $z=1$.

Lo mejor sería hacer una lista de triángulos con un vértice en el centro del círculo. Esto se hace con

disco = Table[Polygon[{z[t], z[t + dt], {2,3, 1}, z[t]}],
              {t, 0,2Pi,dt}];

 

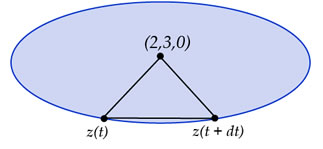
Figura 11.

Usaremos el comando EdgeForm[] para ocultar los bordes y el comando SurfaceColor[] para definir un color para esta superficie.

 

 

Figura 12.

 

 

El código es

 

r = 2; nptos = 30;
dt = (2Pi - 0)/nptos;
z[t_] = {2 +r*Cos[t],3 + r*Sin[t], 1};
circulo = Line[Table[z[t], {t, 0, 2Pi,dt }]];

disco = Table[
                Polygon[{z[t], z[ + dt],
                        {2, 3, 1},
                        z[t]}],
                        {t, 0, 2Pi,dt }
             ];

g = Graphics3D[{
                Ejes3D[-1, 6, -1, 6, -1, 3],
                GrayLevel[0.68],
                AbsoluteThickness[2],  (*Grosor de la linea*)
                circulo,
                EdgeForm[],
                SurfaceColor[RGBColor[0.701961, 0.701961, 1]],
                disco,
                AbsolutePointSize[4],
                RGBColor[1, 0, 0],
                Point[{2, 3, 1}]
                }, Boxed -> False,
                   ViewPoint -> {1.774, 1.815, 2.238}
              ];

Show[g];

Revista digital Matemática, Educación e Internet.
Derechos Reservados