Gráficos 3D

  

Figueroa, G.  Mora, W..

  Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18 

 

Superficies regladas

Una gran cantidad de superficies son generadas por una familia de rectas, a este tipo de superficies se les llama superficies regladas. Dentro de este tipo se superficies se encuentran las superficies cónicas y los cilíndricas.

 

Definición

Un cilindro es el conjunto de todos los puntos que están sobre todas las rectas paralelas a una recta $L$ dada las cuales pasan sobre una curva $C$ que se encuentra sobre un plano $P$. A la recta $L$ se le llama generatriz y a la curva $C$ directriz.


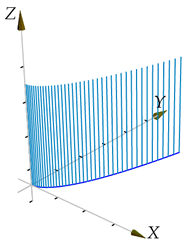
La figura 13.  ilustra la idea que esta detrás de una superficie cilíndrica, en este caso la curva directriz esta sobre el plano $z=0$ y la generatriz es una recta paralela al eje $z$.

 

 

Figura 13.

 

Note que si queremos trazar una porción de una superficie cilíndrica, básicamente lo que debemos hacer es construir una serie de polígonos entre las dos curvas que delimitan dicha porción.


EJEMPLO

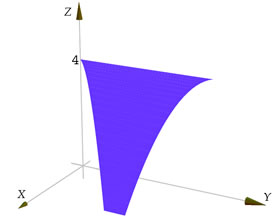
Consideremos el problema de dibujar la porción de la superficie $z=4-x^2$ que se encuentra en el primer octante comprendida entre los planos $y=x$ y $x+y=5$.

Figura 14
[Ver en 3D - JavaView]

 

En este caso la superficie cilíndrica que queremos dibujar es una porción de la superficie $z=4-x^2$. Para esto encontramos las curvas directrices

  • $z = 4 - x^2 \cap y=x \Rightarrow r_1(t)= \left( t,t, 4 - t^2 \right)$.

  • $z = 4 - x^2 \cap x+y=5 \Rightarrow r_2(t)= \left( t,5-t, 4 - t^2 \right)$.

y construimos una serie de polígonos que unen dichas curvas. El código necesario para dibujar la superficies es el siguiente

 

(* Curvas directrices *)

r1[t_] := {t, t, 4 - t^2};

r2[t_] := {t, 5 - t, 4 - t^2};

(* Se generan los poligonos, estos van de r1 hasta r2 *)

dt = 0.1;

polsup = Table[
      Polygon[
        {
          r1[t],
          r2[t],
          r2[t + dt],
          r1[t + dt],
          r1[t]
          }
        ],
      {t, 0, 2, dt}
      ];

(* se construye la grafica *)

sup = Graphics3D[{
                  Ejes3D[0.5, 4, -0.5, 7, -0.5, 6],
                  {EdgeForm[], polsup}
                 },Boxed -> False ];

Show[sup, ViewPoint -> {2.805, 1.489, 1.168}];

 

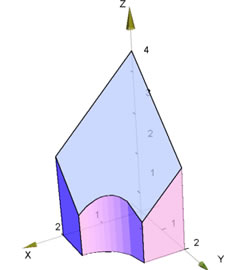
Ahora, podemos usar esta idea para dibujar un sólido cuyas fronteras son superficies cilíndricas, por ejemplo, el sólido del primer octante limitado por las superficies

  • $(x-2)^2 + (y-2)^2 = 1$

  • $x=y=2$

  • $x + y + z = 4$

se muestra en la figura

Figura 15
[Ver en 3D - JavaView]

 

Superficies cónicas

 

Definición (superficie cónica)

Es el conjunto de todos los puntos que están sobre todas las rectas que pasan por una punto fijo llamado vértice y se apoyan sobre una curva directriz.


La figura 1  ilustra la definición de una superficie cónica, en este caso el vértice es un punto sobre el eje $z$ y la directriz es una círculo sobre el plano $z=0$ (únicamente se ha dibujado una rama del cono).

 

Figura 16

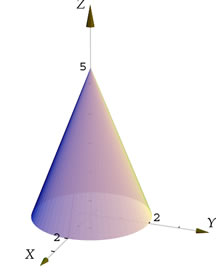
EJEMPLO

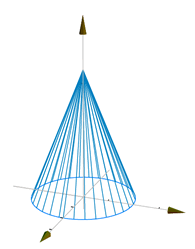
Dibuje el cono con vértice en en punto $(0,0,5)$ y directriz $x^2 + y^2 = 4$.

En este caso construimos un conjunto de poligonos (triángulos ) con dos se sus vértices sobre el círculo $x^2 + y^2 = 4$ y el otro sobre el vértice del cono $(0,0,5)$. El código necesario para generar el cono es el siguiente y su gráfica se muestra en la figura

 

 Figura 17

 

dt = 0.1;
vertice = {0, 0, 5};

r[t_] := {2 Cos[t], 2 Sin[t], 0};

cono = Table[
            Polygon[{
                     r[t],
                     r[t + dt],
                     vertice,
                     r[t]
                    }],
      {t, 0, 2 pi, dt}
      ];

sup = Graphics3D[{Ejes3D[-1, 6, -1, 6, -1, 3],
                  EdgeForm[],
                  cono
                },
       Boxed -> False ];

 

 

Revista digital Matemática, Educación e Internet.
Derechos Reservados