|
|
Se debe tener muy claro cuál es la derivada de cada una de las
funciones trigonométricas estudiadas.
Daremos a continuación la lista de las fórmulas:
| |
|
| 1. |
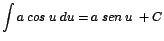 |
| |
Si
 entonces entonces
 por lo que por lo que |
| |
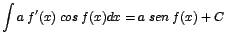 |
Ejemplos
| a. |
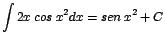 |
| |
Note que
 |
| |
|
| b. |
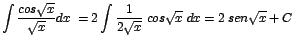 |
| |
Note que
 y y
 |
| |
|
| c. |
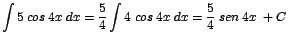 |
| |
|
| d. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
| |
|
| e. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
| |
|
Ejemplos
| |
|
|
d. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
|
e. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
Ejemplos
| a. |
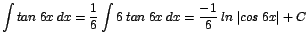 |
| |
|
| b. |
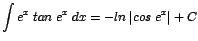 |
| |
Note que 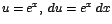 |
| |
|
| c. |
![$\displaystyle {\int \frac{tan \sqrt[3]{x}}{\sqrt[3]{x^{2}}}\;dx}$](img140.gif) Ejercicio para el estudiante Ejercicio para el estudiante |
| |
|
| d. |
 Ejercicio para el estudiante Ejercicio para el estudiante |
| |
|
| 4. |
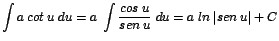 |
| |
Válido para
 |
| |
Si
 entonces entonces
 , por lo que , por lo que
|
| |
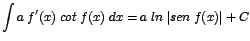 |
Ejemplos
| |
|
|
b. |
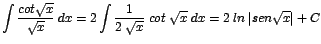 |
| |
|
|
c. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
| |
|
|
d. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
Ejemplos
|
a. |
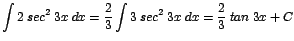 |
Ejemplos
|
a. |
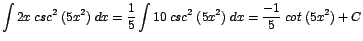 |
| |
|
| b. |
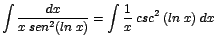 |
| |
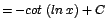 |
|
|
|
| |
|
| d. |
 Ejercicio para el estudiante
Ejercicio para el estudiante |
| |
|
| e. |
 Ejercicio para el estudiante Ejercicio para el estudiante |
| |
|
| 7. |
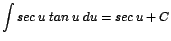 |
| |
Esta igualdad es válida para
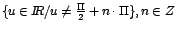 |
| |
Si
 entonces entonces
 , por lo que , por lo que
|
| |
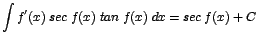 |
Ejemplos
| a. |
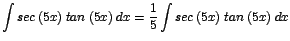 |
| |
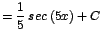 |
| |
|
| b. |
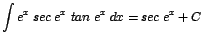 |
| |
|
| c. |
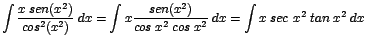 |
| |
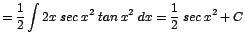 |
| |
|
| d. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| e. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| 8. |
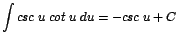 |
| |
Esta igualdad vale para
 |
| |
Si
 entonces entonces
 , por lo que , por lo que
|
| |
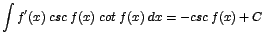 |
Ejemplos
| a. |
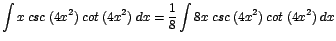 |
| |
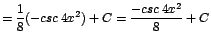 |
| |
|
| b. |
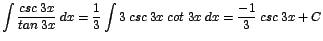 |
| |
|
| c. |
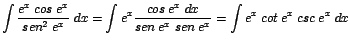 |
| |
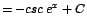 |
| |
|
| d. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| e. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| 9. |
Calculemos ahora
 . Para ello se multiplica el la . Para ello se multiplica el la
|
| |
numerador y el denominador por la expresión
 en en |
| |
forma siguiente: |
| |
|
| |
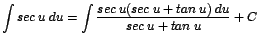 |
| |
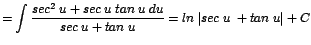 |
| |
Según lo estudiado sobre la integral que da como resultado la
función logaritmo natural, ya que si
 entonces
entonces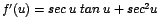 |
| |
y se tiene por tanto
una integral de la forma
 |
| |
El resultado anterior es válido para:
|
| |
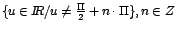 |
| |
Si
 entonces entonces
 , por lo que: , por lo que:
|
| |
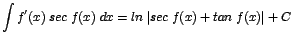 |
Ejemplos
| a. |
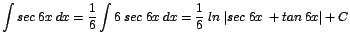 |
| |
|
| b. |
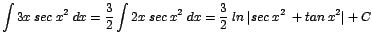 |
| |
|
| c. |
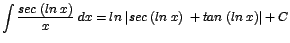 |
| |
|
| d. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| e. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| 10. |
En forma similar al procedimiento seguido en el caso anterior |
| |
calcularemos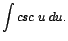 |
| |
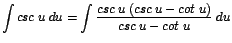 |
| |
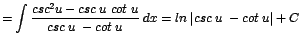 |
| |
Este resultado es válido para
 |
| |
Si
 entonces entonces
 , por lo que: , por lo que:
|
| |
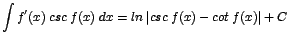 |
Ejemplos
| a. |
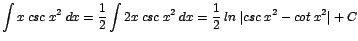 |
| |
|
| b. |
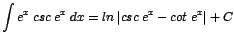 |
| |
|
| c. |
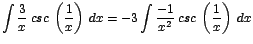 |
| |
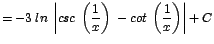 |
| |
|
| d. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
| |
|
| e. |
 Ejercicio para el estudiante Ejercicio para el estudiante
|
Volver
Revista digital Matemática, Educación e Internet.
|