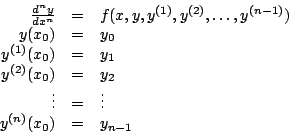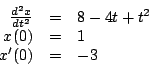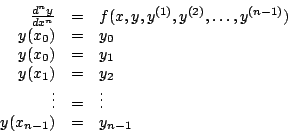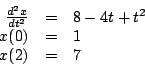|
Problemas de valor inicial y de frontera
En la mayoría de las aplicaciones estamos interesados no en la
solución general de una ecuación diferencial, sino en una
solución particular que satisfaga
ciertas condiciones dadas. Esto da origen a los problemas de valor
inicial o de frontera.
|
|
Definición
[ Problema de valor inicial] |
| |
Un problema de valor inicial o de Cauchy
consta de una ecuación diferencial de orden 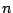 y de y de 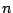 condiciones iniciales impuestas a la función desconocida y a sus
condiciones iniciales impuestas a la función desconocida y a sus
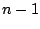 primeras derivadas en un valor de la variable independiente.
Es decir primeras derivadas en un valor de la variable independiente.
Es decir
|
Es decir
Ejemplo
Una partícula 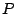 se mueve a lo largo del eje se mueve a lo largo del eje 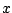 de manera tal
que su aceleración en cualquier tiempo de manera tal
que su aceleración en cualquier tiempo 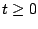 está dada
por está dada
por
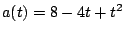 . Encuentre la posición . Encuentre la posición 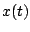 de la
partícula en cualquier tiempo de la
partícula en cualquier tiempo 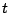 , suponiendo que inicialmente
la partícula está localizada en , suponiendo que inicialmente
la partícula está localizada en 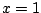 y está viajando a una
velocidad de y está viajando a una
velocidad de 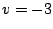 . .
Recuerde que la primera derivada de la posición nos da la
velocidad y la segunda derivada la aceleración. De donde el
problema de valor inicial sería
Integrando con respecto a 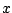 obtenemos obtenemos
y usando la condición 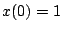 podemos hallar que podemos hallar que 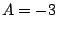 , con
lo cual la velocidad en cualquier tiempo , con
lo cual la velocidad en cualquier tiempo 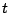 sería sería
Integrando de nuevo
y usando la condición
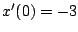 podemos determinar que podemos determinar que
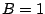 y obtener la posición de la partícula en cualquier
tiempo y obtener la posición de la partícula en cualquier
tiempo 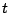
En la figura 7 se muestra la gráfica de la
posición de la partícula versus tiempo.
Figura 7
Ejemplo
Una familia de curvas tiene la propiedad de que la pendiente de la
recta tangente en el punto 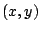 está dada por está dada por 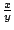 .
¿ Hallar el miembro de esta familia que pasa por el punto .
¿ Hallar el miembro de esta familia que pasa por el punto 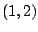 ?
?
El problema de valor inicial asociado es
Para resolver la ecuación diferencial debemos separar variables
e integrar
Y usando la condición inicial 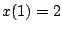 obtenemos que obtenemos que 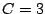 , con
lo cual la curva buscada es , con
lo cual la curva buscada es 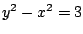 , la cual se muestra en
la figura 8. , la cual se muestra en
la figura 8.
Figura 8
|
|
Definición
[ Problema de valor
frontera] |
| |
Un problema de valores en la frontera o de Dirichlet
consta de una ecuación diferencial
ordinaria de orden 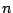 y de y de 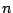 condiciones de frontera impuestas
sobre la función desconocida en condiciones de frontera impuestas
sobre la función desconocida en 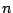 valores de la variable independiente. valores de la variable independiente. |
.Es decir
Ejemplo
Una partícula 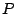 se mueve a lo largo del eje se mueve a lo largo del eje 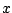 de manera tal
que su aceleración en cualquier tiempo de manera tal
que su aceleración en cualquier tiempo 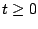 está dada
por está dada
por
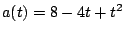 . Encuentre la posición . Encuentre la posición 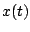 de la
partícula en cualquier tiempo de la
partícula en cualquier tiempo 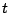 , suponiendo que inicialmente
la partícula está localizada en , suponiendo que inicialmente
la partícula está localizada en 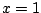 y en y en 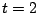 está en está en
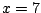 . .
El problema de valores de frontera asociado es
Integrando dos veces obtenemos que la posición de la partícula
está dada por
Evaluando las condiciones de frontera obtenemos el siguiente sistema
de donde 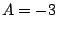 y y 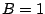 . Y así la posición de la partícula
en cualquier tiempo está dada por . Y así la posición de la partícula
en cualquier tiempo está dada por
La gráfica de la posición 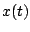 se muestra en la figura
7. se muestra en la figura
7.
Revista digital Matemática, Educación e Internet.
|