|
Soluciones singulares
|
|
Definición
[ Solucion singular de una
ecuación diferencial] |
| |
Una solución de una ecuación diferencial se llama singular
si no se puede obtener de la
solución general al sustituir las constantes por valores, es
decir, no es una solución particular.
|
Ejemplo
La familia de rectas 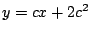 es la solución general de
la ecuación diferencial es la solución general de
la ecuación diferencial
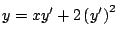 . La parábola . La parábola 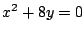 es una solución
singular. es una solución
singular.
No es difícil comprobar que ambas son solución de la
ecuación diferencial dada. En la figura
3 se
muestra la solución singular y varias soluciones particulares.
Figura 3
Observe que la parábola es tangente en cada uno de sus puntos a
una curva de la familia de rectas 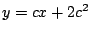 , cuando sucede
esto decimos que la parábola , cuando sucede
esto decimos que la parábola 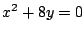 es la envolvente de la
familia de rectas es la envolvente de la
familia de rectas 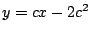 ; como se indica en la siguiente
definición. ; como se indica en la siguiente
definición.
|
|
Definición
[Envolvente] |
| |
Cualquier curva tangente a un número infinito de miembros de una
familia infinita de curvas, y que por lo menos es tangente en cada
uno de sus puntos a una de dichas curvas, es una parte, o el
total, de la envolvente de la familia.
|
La envolvente de una familia de curvas 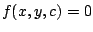 satisface el sistema satisface el sistema
lo cual nos permite hallarla.
Ejemplo
Para hallar la envolvente de la familia de circunferencias
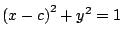 , resolvemos el sistema , resolvemos el sistema
obteniendo que 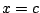 . Al sustituir en la ecuación de la familia
obtenemos que la envolvente está formada por
las rectas . Al sustituir en la ecuación de la familia
obtenemos que la envolvente está formada por
las rectas 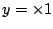 . La envolvente y algunos miembros de la
familia se muestran en la figura 4. . La envolvente y algunos miembros de la
familia se muestran en la figura 4.
Figura 4
Ejemplo
La familia de parábolas 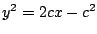 es la solución general
de la ecuación diferencial es la solución general
de la ecuación diferencial
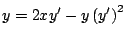 y las rectas y las rectas 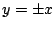 son soluciones singulares. son soluciones singulares.
Fácilmente se comprueba que ambas son soluciones de ecuación
diferencial. En la figura 5 se muestran las
soluciones singulares y varias soluciones particulares. Las rectas
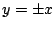 son la envolvente de la familia de parábolas son la envolvente de la familia de parábolas
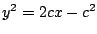 . .
Figura 5
Subsecciones
Revista digital Matemática, Educación e Internet.
|