|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1   2   3   4   5   6   7   8   9   10      

 

 

 

  ¿ Qué es una ecuación diferencial ?

 

	Definición  [Ecuación Diferencial]
	Una ecuación diferencial (ED) es una ecuación que relaciona de manera no trivial a una función desconocida y una o más derivadas de esta función desconocida con respecto a una o más variables independientes. Si la función desconocida depende de una sola variable la ecuación diferencial se llama ordinaria , por el contrario, si depende de más de una variable, se llama parcial .

La frase de manera no trivial que hemos usado en la definición anterior tiene como propósito descartar ecuaciones diferenciales que satisfacen la definición, pero son realmente identidades, es decir, son siempre verdaderas sin importar quién sea la función desconocida. Un ejemplo de tal tipo de ecuaciones es:

$$Sin^2 \left( \frac{dy}{dx} \right) + Cos^2 \left( \frac{dy}{dx} \right) = 1$$

Esta ecuación es satisfecha por cualquier función en una variable que sea derivable. Otro ejemplo es

$$\left( \frac{dy}{dx} - y \right)^2 = \left( \frac{dy}{dx} \right)^2 - 2 y \frac{dy}{dx} + \left( \frac{dy}{dx} \right)^2$$

Es claro que lo que está detrás de esta ecuación es la fórmula notable $\left( a + b \right)^2 = a^2+ 2ab + b^2$; por lo que la ecuación es satisfecha por cualquier función derivable.

Nuestra atención se centrará sobre ecuaciones diferenciales ordinarias . Una ecuación diferencial ordinaria es aquella que tiene a $y$ como variable dependiente y a $x$ como variable independiente se acostumbra expresar en la forma

$$F(x,y,y^{(1)}, y^{(2)}, \ldots, y^{(n)}) = 0$$ (1.4)

para algún entero positivo $n$. Si podemos despejar de esta ecuación la derivada más alta, obtenemos una o más ecuaciones de orden $n$ de la forma

$$y^{(n)} = G(x,y,y^{(1)}, y^{(2)}, \ldots, y^{(n-1)} )$$

 

Ejemplo
La ecuación $\left(y^{\prime} \right)^2 + xy^{\prime} - =0$ es equivalente a las dos ecuaciones diferenciales

$$\begin{array}{ccc} y^{\prime} = \frac{\sqrt{x^2 + 4y}-x}{2... ...} & y^{\prime} = \frac{-\sqrt{x^2 + 4y} - x }{2} \end{array}$$

Las ecuaciones diferenciales se clasifican en varias categorías, como ya vimos, según su tipo en ordinarias y parciales, o según su linealidad u orden, como veremos.

 

	Definición  [ Orden de una ecuación diferencial]
	El orden de una ecuación diferencial es igual al de la derivada de más alto orden que aparece de manera no trivial en la ecuación.

 

De nuevo, la frase de manera no trivial tiene el fin de evitar situaciones como la siguiente

$$\left( \frac{d^3 y}{dt^3} \right)^{\frac{1}{3}} + y = e^x$$

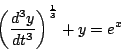
cuyo orden es uno y no tres, como podría pensarse.

 

	Definición  [Ecuación Diferencial lineal]
	Una ecuación diferencial ordinaria de orden $n$ es lineal  si se puede escribir de la forma $$a_n(x) y^{(n)} + a_{n-1}(x) y^{(n-1)} + \ldots + a_1(x) y^{(1)} + a_0(x) y = g(x)$$ (1.5) donde los coeficientes $a_k(x)$ para $k=0,1, \ldots, n$ son funciones reales, con $a_n(x) \neq 0$. Una ecuación diferencial ordinaria que no se pueda expresar de esta forma es no lineal.

 

Algunas veces decimos que la ecuación 1.5 es lineal con coeficientes constantes si las funciones $a_k(x)$ son constantes para toda $k$, en caso contrario, decimos que es con coeficientes variables. Por otro lado, si la función $g(x)$ es nula decimos que la ecuación diferencial ordinaria lineal es homogénea y en caso contrario no homogénea. Todos estos tipo se ecuaciones diferenciales serán estudiados posteriormente con más detalle.

 

Ejemplo
La ecuación diferencial

$$\frac{dy}{dt} = \frac{2p}{\sqrt{n}} y^{\frac{3}{2}} \left( 1-y \right)^{\frac{3}{2} }$$

es de primer orden, no lineal y no homogénea. Esta ecuación surge en sicología y representa un modelo del aprendizaje. La variable $y$ representa el nivel de habilidad del individuo como una función del tiempo $t$. Las constantes $p$ y $n$ dependen del individuo considerado y de la naturaleza de la tarea que se este aprendiendo.

 

Ejemplo
La ecuación

$$L \frac{d^2q}{dt^2} + R \frac{dq}{dt} + \frac{1}{C} q = E(t)$$

es de segundo orden, lineal con coeficientes constantes y no homogénea. Esta ecuación diferencial surge en el estudio de circuitos eléctricos que consisten de un inductor $L$, un resistor $R$ y un capacitor $C$, al cual se aplica una fuerza electromotriz $E(t)$.

 

Ejemplo  
La ecuación

$$y^{(3)} + 3 y^{(2)} - 5y = 0$$

es de orden 3, lineal con coeficientes constantes y homogénea.

La ecuación

$$x \left( y^{\prime \prime} \right)^2 + y^{\prime} = Cos(xy)$$

es de primer orden, no lineal y no homogénea.

La ecuación

$$\left(x^2 + 1 \right) y^{\prime \prime} + Sen(x) y^{\prime} + 6y = xCos(x)$$

es de segundo orden, lineal con coeficientes variables y no homogénea.

El concepto de orden también se extiende a las ecuaciones parciales como se muestra en el siguiente ejemplo.

 

Ejemplo  

La ecuación

$$\frac{\partial u}{\partial t} = c^2 \frac{\partial^2 u}{ \partial x^2}$$

se conoce como la ecuación de calor y es de primer orden en $t$ y de segundo orden en $x$.

La ecuación

$$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0$$

se conoce como la ecuación de Laplace y es de segundo orden en $x$ e $y$.

La ecuación

$$c^2 \left( \frac{\partial^2 u}{\partial x^2} + \frac{\parti... ... u}{\partial y^2} \right) = \frac{\partial^2 u}{\partial t^2}$$

se conoce como la ecuación de onda y segundo orden en $x$, $y$ y $t$.

Las ecuaciones de Laplace, de calor y de onda poseen un importante significado en física teórica y su estudio ha estimulado el desarrollo de muchas ideas matemáticas relevantes. En general, las ecuaciones diferenciales parciales aparecen en problemas relacionados con campos eléctricos, dinámica de fluidos, difusión y movimiento ondulatorio. Su teoría es muy diferente de la de las ecuaciones diferenciales ordinarias y notablemente más difícil en casi todas sus facetas.

Subsecciones

• Ejercicios

  

- Revista virtual Matemática, Educación e Internet - ITCR