|
Solución numérica
Para facilitar el trabajo y evitar la tarea de programación del método, podemos
usar una hoja de cálculo como Microsoft Excel (en Windows) o Gnumeric (en Linux).
Veamos el siguiente ejemplo
Ejemplo
Una resistencia de 5 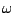 y un inductor de 1 Henrio se conectan en serie con
un generador de y un inductor de 1 Henrio se conectan en serie con
un generador de 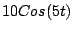 voltios. Si la corriente es 0 en voltios. Si la corriente es 0 en 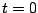 , ¿ calcule la
la corriente en el instante , ¿ calcule la
la corriente en el instante 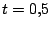 segundos ? segundos ?
Usando las ley de Kirchhoff modelamos la situación anterior con el siguiente problema de valor inicial
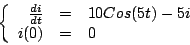 |
(1.14) |
Fácilmente podemos comprobar que su solución general esta dada por
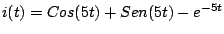 , con lo cual , con lo cual
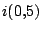 es aproximandamente igual a es aproximandamente igual a 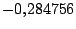 . .
Ahora vamos usar una hoja de cálculo y el método de Euler para aproximar
la solución del problema de valor inicial anterior.
Primero pongamonos de acuerdo con los contenidos de cada columna
- La columna A representará el tiempo
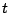 . .
- La columna B representará la aproximación de la corriente
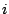 ,
dada por el método de Euler. ,
dada por el método de Euler.
- La celda C representará el paso de avance
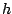 . .
Ahora coloquemos los valores iniciales en la celda correspondiente
- En la celda A2 escribimos el valor inicial del tiempo, en nuestro caso 0,
- En la celda B2 escribimos el valor inicial de la corriente, es decir, 0
- En la celda C2 escribimos el valor de
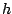 , digamos 0.01. , digamos 0.01.
- En la celda A3 escribimos la fórmula que construirá los
valores de
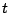 , es decir, =A2 + C$2 y arrastramos ésta celda hasta
alcanzar el valor de , es decir, =A2 + C$2 y arrastramos ésta celda hasta
alcanzar el valor de 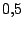 . .
- En la celda B3 escribimos la fórmula que construirá la sucesión
de valores para
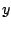 , es decir, =B2 + C$2*(10*Cos(5*A2) - 5*B2) y la arrastramos hasta
alcanzar el valor de , es decir, =B2 + C$2*(10*Cos(5*A2) - 5*B2) y la arrastramos hasta
alcanzar el valor de 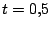 en la columna A (el signo de dólares $ se usa
para evitar que el valor se actualize conforme arrastramos la
celda). en la columna A (el signo de dólares $ se usa
para evitar que el valor se actualize conforme arrastramos la
celda).
Una vez generados los valores para las columnas A y B
podemos observar que
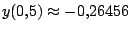 que es similar al
valor real ya encontrado ( que es similar al
valor real ya encontrado (
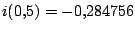 ) . En la figura
10
se muestra este proceso junto con una gráfica de la solución aproximada
obtenida a partir de las columnas A y B y en el mismo
sistema de coordenadas la gráfica de la solución exacta ) . En la figura
10
se muestra este proceso junto con una gráfica de la solución aproximada
obtenida a partir de las columnas A y B y en el mismo
sistema de coordenadas la gráfica de la solución exacta
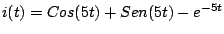 . .
Figura 10
Usar una hoja de cálculo para aproximar la solución de una
ecuación diferencial resulta sencillo, pero existen muchas otras
opciones que podemos usar. El siguiente código muestra una función
implementada para la TI92 que calcula el valor aproximado de
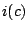 para el problema de valor inicial anterior
(1.14) para el problema de valor inicial anterior
(1.14)
euler(a,b,c,h)
Func
local x0, y0,
While x0 < c
y0 + h*f(x0,y0) -> y0
x0 + h -> x0
EndWhile
Return y0
EndFunc
Antes de usar la función Euler debemos definir la
función
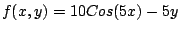 ; y para ejecutarla escribimos en la
ventana Home: euler(0,0,0.5,0.01). Al hacerlo obtenemos el
valor ; y para ejecutarla escribimos en la
ventana Home: euler(0,0,0.5,0.01). Al hacerlo obtenemos el
valor
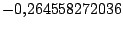 que está muy cerca de valor real. que está muy cerca de valor real.
- Revista virtual
Matemática, Educación e Internet -
ITCR
|