|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1   2   3   4   5   6   7   8   9   10  

Ecuación diferencial de una familia de curvas En esta sección discutimos un poco acerca del proceso inverso que nos ocupará a lo largo del curso. Recuerde que nuestro objetivo principal es determinar la solución general de una ecuación diferencial, la cual es una familia de curvas , sin embargo, ahora trataremos de determinar una ecuación diferencial cuya solución general sea una familia de curvas dada. Dada una familia de curvas $n$-paramétrica $f(x,y,c_1,c_2, \ldots,c_n)=0$, la idea básica es eliminar las $n$ constantes $c_i$, para esto derivamos $n$ veces la ecuación de la familia y formamos el siguiente sistema $$\begin{array}{rcl} f(x,y,c_1,c_2,\ldots,c_n & = & 0 \\ f... 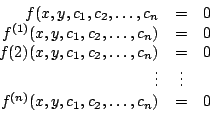...\ f^{(n)}(x,y,c_1,c_2,\ldots, c_n) & = & 0 \\ \end{array}$$ a partir del cual podemos obtener la ecuación diferencial buscada.   Ejemplo   Determine una ecuación diferencial cuya solución general sea la familia de curvas $$y=A Sen(x)+ B Cos(x)$$ (1.6) Derivando dos veces la ecuación de la familia (1.6), obtenemos $$\begin{array}{rcl} y^{\prime} & = & A Cos(x) - B Sen(x) \\ y^{\prime \prime} & = & -A Sen(x) - B Cos(x) \\ \end{array}$$ Y observe que $y^{\prime \prime } + y = 0$ es la ecuación diferencial  buscada.   Observación Dada una familia de curvas $n$-paramétrica, por lo general es fácil obtener una ecuación diferencial de orden mayor $n$ que tenga a ésta familia como solución. Por ejemplo, $y=c_1 + c_2 x^3$ sería una solución de la ecuación diferencial de cuarto orden $y^{(4)} = 0$, pero por supuesto que esta no es la solución general de la ecuación diferencial. Algunas veces la familia de curvas se nos presenta en forma de un enunciado a partir del cual debemos obtener la ecuación, como muestran los siguientes ejemplos.   Ejemplo  Encontrar una ecuación diferencial cuya solución general sea la familia de círculos con centros sobre la recta $y=x$ y tangentes al eje $y$. La familia de círculos se muestra en la figura 6. Observe que por estar centrados sobre la recta $y=x$ los círculos también deben ser tangentes al eje $x$.   Figura 6 Como los círculos están centrados en $(A,A)$ y tienen radio $A$, la ecuación de la familia sería $$\left(x - A \right)^2 + \left(y - A \right)^2 = A^2$$ (1.7) Desarrollando las fórmulas notables obtenemos $$x^2 - 2Ax + A^2 + y^2 - 2Ay + A^2 = A^2$$ Derivando implícitamente con respecto a $x$ $$2x - 2A + 2yy^{\prime} - 2A = 0$$ (1.8) Despejando $A$ de la ecuación 1.8 y sustituyéndolo en el ecuación de la familia 1.7 obtenemos la ecuación diferencial buscada $$x^2 - 4xy + 4y^2 - y^{\prime} \left( 2xy - 4y^2 \right) + y^2 \left( y^{\prime} \right)^2 = 0$$   Ejemplo  Encontrar una ecuación diferencial cuya solución general sea la familia de círculos con radio 1 y centro en $(A,B)$. La ecuación de la familia de círculos con centro en $(A,B)$ y radio 1 es $$\left(x - A \right)^2 + \left(y - B \right)^2 = 1$$ (1.9) Derivando implícitamente respecto a $x$ $$2 \left(x - A \right) + 2 \left(y - B \right) y^{\prime} = 0$$ (1.10) Despejando el término $\left(X - A \right)$ de la ecuación (1.10) y sustituyéndolo en la ecuación de la familia (1.9) obtenemos $$\left(y - B \right)^2 \left(y^{\prime} \right)^2 + \left(y - B \right)^2 = 1$$ la cual no contiene a constante $A$. Para eliminar la constante $B$, despejemos el término $\left( y - B \right)$ $$y - B = \pm \left(1 + \left( y^{\prime} \right)^2 \right)^{\frac{1}{2}}$$ De donde, derivando implícitamente y simplificando obtenemos la ecuación diferencial deseada $$\frac{y^{\prime \prime}}{1 + \left(y^{\prime} \right)^2} = \pm 1$$ (1.11) Observe que el lado derecho de la ecuación (1.11) es la fórmula de curvatura y efectivamente la curvatura de los círculos es 1. Subsecciones Ejercicios   Revista digital Matemática, Educación e Internet.