|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1   2   3   4   5   6   7   8   9   10  

 

 

 

  Solución de una ecuación diferencial

 

	Definición  [ Solucion de una ecuación diferencial]
	Decimos que $y=g(x)$ es una solución de la ecuación diferencial 1.4, en el intervalo $I$ si $$F(x,y,g(x),g^{(1)}(x),\ldots, g^{(n)}(x)) = 0$$

para toda $x \in I$. Es decir, una solución, es una función $g(x)$ definida en algún intervalo $I$ que al sustituirla en la ecuación la transforma en una identidad para todo $x \in I$.

 

Ejemplo
La función $y = \sqrt{4-x^2}$ es solución de la ecuación diferencial ordinaria $y^{\prime} = -\frac{x}{y}$ para toda $x \in ]-2,2[$.

Derivando la función $y$ obtenemos que

$$y^{\prime} = - \frac{x}{\sqrt{4-x^2} } = - \frac{x}{y}$$

 

Ejemplo
La función $y = e^{-x} + x -1$ es solución de la ecuación diferencial $y^{\prime} +y = x$ para toda $x \in \mbox{$I \hspace{-1.3mm} R$}$.

Derivando la función $y$ y sustituyendo obtenemos que

$$y^{\prime} + y = -e^{-x} + 1 + e^x + x - 1 = x$$

 

Ejemplo  
La función $u(x,y) = \frac{x^3}{3}e^y + 2xe^y - 2x$ es solución de la ecuación diferencial parcial

$$\frac{\partial^2 u}{\partial x \partial y} = \frac{\partial u}{\partial x} + 2$$

en todo $R^2$.

Calculando las derivadas parciales

$$\frac{\partial u}{\partial x} = x^2e^y + 2e^y -2$$

$$\frac{\partial^2 u}{\partial x \partial y} = x^2e^y + 2e^y$$

Al sustituir obtenemos una igualdad

$$\frac{\partial u}{\partial x} + 2 = x^2e^y + 2 e^y -2 + 2 = x^2 e^y + 2e^y = \frac{\partial^2 u}{\partial x \partial y}$$

Recuerde que no toda ecuación diferencial que se nos ocurra tiene solución, por ejemplo, para la ecuación diferencial

$$\left( \frac{dy}{dx} \right) + y^2 = -1$$

no existe una función real derivable que la satisfaga, pues el lado derecho es negativo y el lado izquierdo positivo. De aquí en adelante vamos a suponer que las soluciones que buscamos son reales y que el intervalo $I$ es el adecuado que permita que la solución tenga sentido.

 

Ejemplo  
La función $y^3 -3x+3+3y=5$ es una solución de la ecuación $y^{\prime \prime} = -2y \left( y^{\prime} \right)^3$.

Derivando implícitamente con respecto a $x$, obtenemos

$$3y^2 y^{\prime} - 3 + 3 y^{\prime} = 0 \Rightarrow y^{\prime} = \frac{1}{y^2 + 1}$$

Derivando implícitamente de nuevo, para calcular la segunda derivada

$$y^{\prime \prime} = - \frac{2y y^{\prime}}{\left( y^2 + 1 \... ...2y}{\left(y^2 + 1 \right)^3} = -2y \left(y^{\prime} \right)^3$$

Hasta este momento hemos visto ejemplos en los cuales la solucióón esta dada en formas explícita o implícita. En los siguientes ejemplos se muestran situaciones un tanto diferentes.

 

Ejemplo  
La curva dada en forma paramétrica por

$$\left\{ \begin{array}{rcl} x & = & te^t \\ y & = & e^{-t} \\ \end{array} \right.$$

es solución de la ecuación diferencial $\left(1 + xy \right) y^{\prime} + y^2 = 0$.

Calculemos $y^{\prime}$

$$y^{\prime} = \frac{dy}{dx} = \frac{ \frac{dy}{dt} }{ \frac{dx}{dt} } = \frac{-e^{-t}}{e^t + te^t}= \frac{-e^{-2t}}{1+t}$$

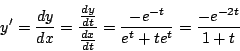
Sustituyendo

$$\left( 1+ xy \right) y^{\prime} + y^2 = \left(1 + t \right) \frac{-e^{-2t}}{1+t} + e^{-2t} = -2e^{-2t} + 2e^{-2t} = 0$$

 

Ejemplo  

La función

$$y = x \int_0^x \frac{Sen(t)}{t} dt + 4$$

es solución de la ecuación diferencial $xy^{\prime} = y + x Sen(x)$.

Observe que para calcular $y^{\prime}$ debemos usar el teorema fundamental del cálculo^1.2

$$y^{\prime} = \int_0^x \frac{Sen(t)}{t} dt + Sen(x)$$

Sustituyendo

$$xy^{\prime} = x \left( \int_0^x \frac{Sen(t)}{t} dt + Sen(t) \right) = y + xsen(x)$$

Si la solución de una ecuación diferencial de orden $n$ tiene $n$ constantes diferentes, diremos que dicha solución es la solución general de la ecuación diferencial . Si asignamos valores a algunas o todas esas constantes obtenemos lo que se conoce como una solución particular .

 

Ejemplo  

La familia de curvas $y = ASen(x) + BCos(x)$ es la solución general de la ecuación diferencial $y^{\prime \prime } + y = 0$, mientras que $y=2Sen(x) + 3Cos(x)$ y $y=ASen(x)$ son soluciones particulares.

Algunas veces, a una solución de una ecuación diferencial se le llama integral de la ecuación y a su gráfica curva integral o curva solución. Como la solución general de una ecuación diferencial de orden $n$ tiene $n$ constantes se acostumbra llamarla familia n-paramétrica de soluciones y se denota por $G(x,y,c_1,c_2,\ldots,c_n)=0$. Esto quiere decir que una ecuación diferencial tiene una cantidad infinita de soluciones que corresponden a la elección ilimitada de esos paramétros.

 

Ejemplo  

La familia de parábolas $y^2=2xc-c^2$ es la solución general de la ecuación diferencial $y=2xy^{\prime} -y \left( y^{\prime} \right)^2$.

Derivando implícitamente

$$2yy^{\prime} = 2c \Rightarrow y y^{\prime} = c$$

Sustituyendo

$$2xy^{\prime} -y \left( y^{\prime} \right)^2= 2xy^{\prime} -... ...y} \left(2x - c \right) = \frac{2cx-c^2}{y}= \frac{y^2}{y}= y$$

En la figura 2 se muestran algunas curvas solución.

 

Figura 2

Subsecciones

• Ejercicios

 

Revista digital Matemática, Educación e Internet.