|
|
Ejercicios
- Use el teorema de existencia y unicidad para determinar si
existen soluciones únicas para cada uno de los siguientes
problemas de valores iniciales
-
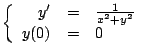
-
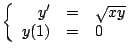
-
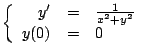
-
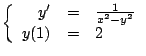
- Muestre que
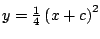 y y 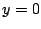 son soluciones de la ecuación diferencial
son soluciones de la ecuación diferencial
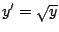 . Discuta sobre la relación de estas soluciones con el
teorema de existencia y unicidad. . Discuta sobre la relación de estas soluciones con el
teorema de existencia y unicidad.
- Determine una región
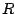 del plano del plano 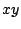 para la cual la
ecuación diferencial para la cual la
ecuación diferencial
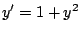 tenga solución
única en el punto tenga solución
única en el punto 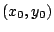 . .
- Determine los valores de
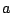 y y 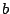 de forma que el problema de valor inicial de forma que el problema de valor inicial
- ¿ Que dice el teorema de existencia unicidad respecto a la solución del problema de valor inicial
- Revista virtual
Matemática, Educación e Internet -
ITCR
|