|
|
Ejercicios
- Compruebe si expresión dada es solución de la ecuación
diferencial. Donde sea adecuado suponga que
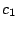 y y 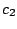 son
constantes. son
constantes.
-
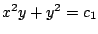
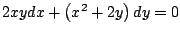
-
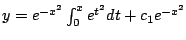
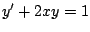
-
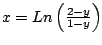
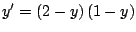
-
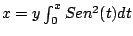
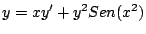
-
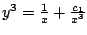
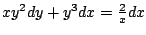
-
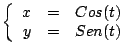
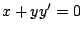
-
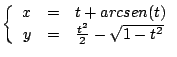
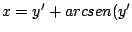
-
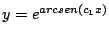
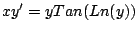
-
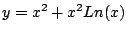 con con 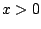
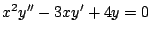
-
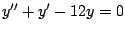
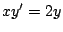
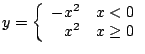
-
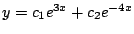
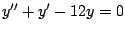
- Para cada una de las siguientes ecuaciones diferenciales
encuentre el valor o valores de
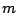 de forma tal que de forma tal que 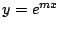 sea una solución de la ecuación diferencial dada.
sea una solución de la ecuación diferencial dada.
-
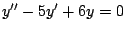
-
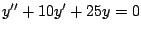
-
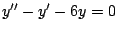
- Para cada una de las siguientes ecuaciones diferenciales
encuentre el valor o valores de
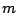 de forma tal que de forma tal que 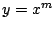 sea
una solución de la ecuación diferencial dada. sea
una solución de la ecuación diferencial dada.
-
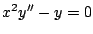
-
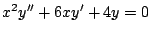
- Revista virtual
Matemática, Educación e Internet -
ITCR
|